
我有幸与心理博弈教练Jared Tendler共事多年,并与他合著了《扑克心理博弈》一书。在他给予我的所有建议中,最令我难忘的是关于如何度过学习迷茫期的指导——那还是在求解器问世之前的年代,我们尚未拥有如今能精准定位技术漏洞的工具。他的建议是:
若不知从何学起,就专攻你的C Game状态。
他的意思是:找出你最严重的失误,并努力纠正。最严重的失误往往让你损失最多资金,造成最大情绪波动,也最容易被识别。这种方法能让你获得最高的”投入产出比”。
在求解器时代,我的另一位合著者Dara O’Kearney从期望值的角度向我展示了相同的学习方法。某些类型的错误代价更高,而求解器能清晰揭示这一点。如今你可以量化每个错误造成的损失,因此没有理由不优先解决危害最大的问题。
值得庆幸的是,GTO Wizard能精准显示任何错误的代价——在手牌矩阵中,它会以bb为单位展示每个行动的期望值。今天我们将深入探索这一功能,并演示如何利用它来指导学习。
翻牌前错误
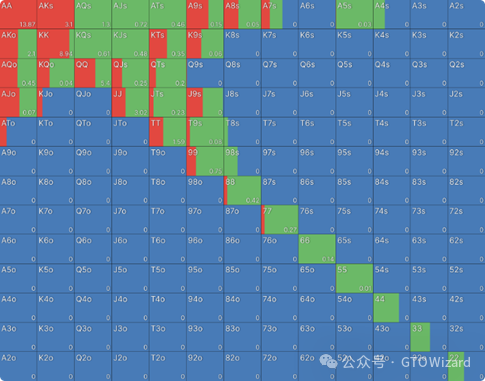
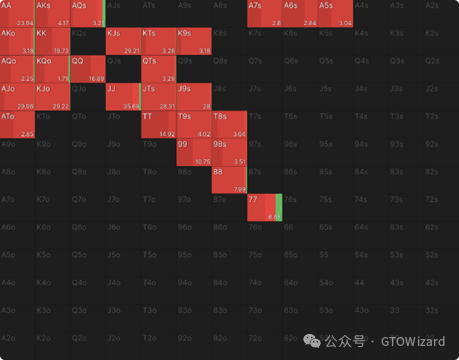
让我们从一个简单示例开始。这是MTT中有效筹码40bb时,UTG位的筹码EV开池范围。
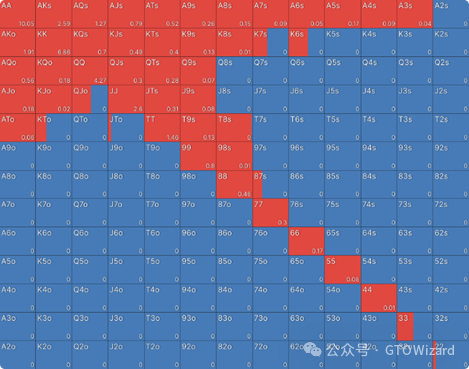
在此矩阵中,您已可直观看到每手牌作为开池牌的总体期望值。显而易见,AA盈利能力极强,平均能带来10.05BB的收益,而44几乎盈亏平衡,仅产生0.01BB收益。至于Q8s等我们不游戏的手牌,其期望值显然为0。
当您将鼠标悬停于特定手牌时,系统将显示该手牌每个可选动作的具体期望值。
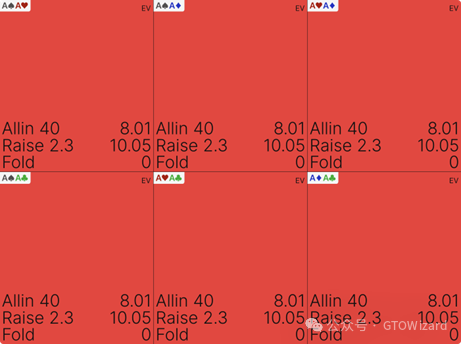
如您所见,用AA全下虽能盈利(平均收益8.01BB),但采用开池策略则能创造更高价值——因为我们希望用如此强牌诱导对手入池,而非将其吓退。
而像Q9s这类手牌,其盈利能力高度依赖决策选择:
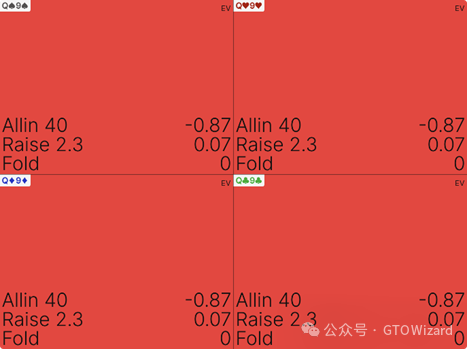
此时开池平均收益为0.07BB,但全下将导致0.87BB的损失——两者差异高达0.94BB。这是因为Q9s这类手牌在翻牌后具有可操作性,但若遭遇再加注我们往往只能弃牌。当我们用Q9s全下时,只会被那些明显领先的牌跟注,使其成为负期望值选择。
这个结论或许显而易见。但更值得探究的是处于边际范围两侧的手牌差异,它能揭示范围底端决策失误的惨重代价。
在此示例中,我们开池范围中最差的不同花Ace是ATo:

ATo作为全下选项同样无利可图,但作为开池手牌能带来0.06BB的平均收益。现在让我们将其与仅差一级牌力却未纳入开池范围的A9o进行对比:

若您在此位置游戏A9o,事后复盘发现这是决策错误时,可能会自我安慰说”差距不大”,认为无伤大雅。
实则谬以千里。
用A9o开池会使我们损失0.08BB。其与ATo的期望值差距达0.14BB。可见在范围底端即使仅偏差一级牌力,代价也相当沉重。对于MTT玩家而言,0.14BB的误差或许听来微不足道,但正如现金桌玩家所知——这类错误在大样本下会产生复利效应。若您始终在该位置犯此错误,长期将导致14bb/100手的巨额漏洞。
细微误差在大量样本中持续累积,最终造成的损失远超您的想象。
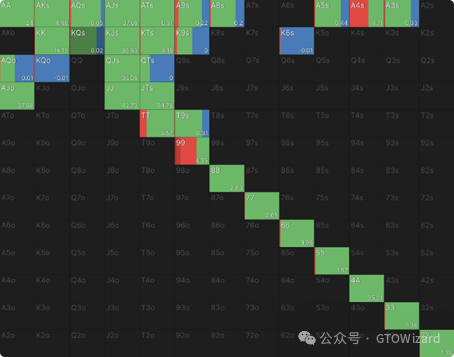
假设UTG采用正确的范围开池,且后续玩家均弃牌至大盲位,其应对策略如下:
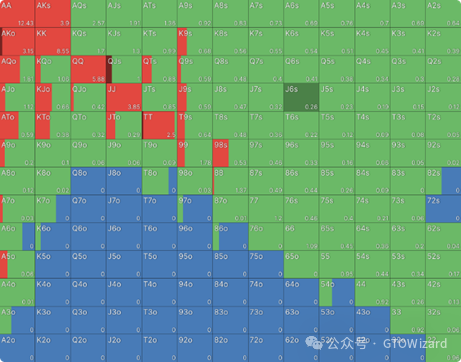
如您所见,BB会用超过一半的范围继续游戏——因为他们获得有利的跟注价格,且享有最终行动权。若您尚未熟悉最小防守频率概念,此刻正是绝佳的学习契机。以J6s这类看似微弱的手牌为例:
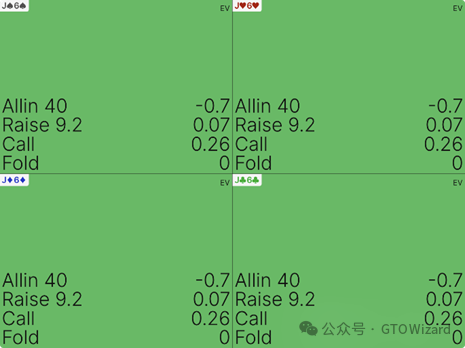
跟注与弃牌之间的期望值差异极为显著——两者相差0.26BB,这甚至超过前例中UTG用错误手牌开池造成的损失。选择弃牌看似”稳妥”,实则是在持续烧钱,这将导致26bb/100手的长期漏洞。
让我们退一步,改用没有盲注投入的响应玩家示例。回到UTG开池的场景,但这次是HJ玩家在斟酌应对策略:
HJ位可跟注的最弱不同花Ace是AJo,该手牌能带来0.07bb的期望收益
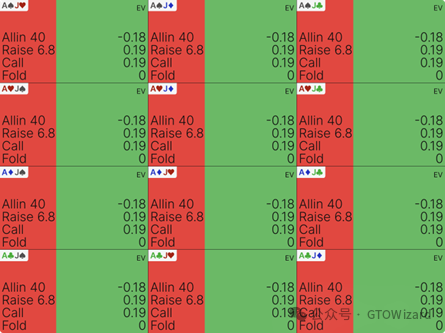
有趣的是,范围外的首手牌仍存在继续游戏的可能——ATo虽从不用于跟注,但偶尔会用于加注

这是因为ATo对抗UTG开池范围表现不佳,但作为诈唬牌却颇具价值——它能阻断对手范围内占比较高的强Ax牌。虽然作为诈唬仅能盈亏平衡,但若用于跟注则会使HJ损失0.11bb。AJo与ATo的跟注期望值差异达0.18bb。可见在范围底端,正确跟注与亏损跟注的差距正在扩大。此处仅一级牌力偏差的错误跟注,在大样本下将导致18bb/100手的损失。这也揭示出:持续游戏方式的决策失误可能造成重大影响。
有些手牌适合下注却不适合跟注,有些适宜开池却不适合全下,反之亦然。GTO Wizard中的期望值输出不仅展示行动的盈利性,更揭示了这些行动背后的策略逻辑。
GTO Wizard中的期望值输出不仅揭示了行动的盈利性,更阐明了这些决策背后的策略逻辑。
回到跟注分析——现在让我们扩大手牌间的差距。例如,若用完全不应继续游戏的A9o进行跟注,结果如下:
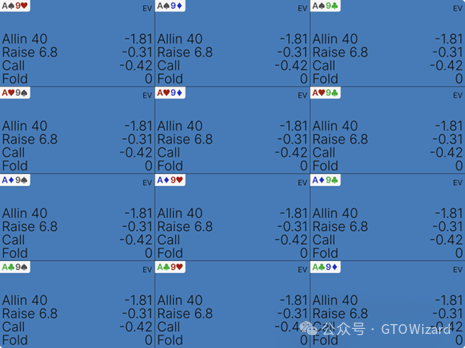
用AJo跟注可盈利0.07BB,而用A9o跟注将损失0.42BB——两者差距已达0.49BB。这一差异极为显著,若持续犯错,在大样本下将导致49bb/100手的巨额漏洞。一级牌力判断失误已属严重,更大偏差则意味着资金的大量流失
翻牌后错误

在此示例中,UTG以40bb有效筹码开池,SB进行3-bet后UTG选择跟注。翻牌发出J♥J♦4♠。在此牌面,SB几乎用整个范围进行下注,且更倾向于选择25%的小尺度下注。
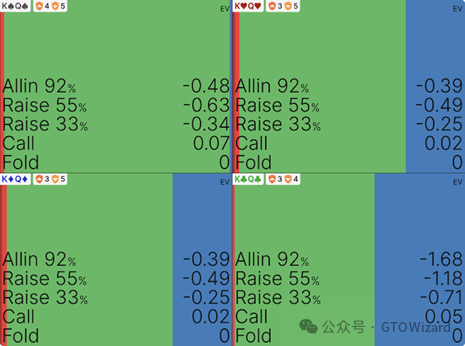
这是典型的范围下注——由于SB持有显著的范围优势,最盈利的策略是以小尺度下注整个范围。通过观察随机手牌样本的各项行动期望值,您可以清晰验证这一点。

无论手持坚果牌、中等牌力还是完全空气牌,最具盈利性的行动都是25%尺度下注。在此类牌面,玩家可能会倾向于用KJs这样的强牌或T8s这样的空气牌采用更大尺度——试图用三条获取更多价值,或迫使对手弃牌——但数据显示这将是决策错误。KJs使用50%底池下注与25%尺度的期望值差异可达0.31BB,相当于31bb/100手的长期漏洞。这看似细微偏差,实为重大失误。
假设我们执行25%底池下注,UTG的应对策略如下:
由于下注尺度较小,且此类牌面双方牌力都难有提升,因此多数手牌会选择继续游戏——翻前牌力强度在此占据主导因素。跟注范围中最弱的手牌包括KQs,该手牌能带来0.07bb的期望收益。
少数弃牌手牌中包含KQo——该手牌可能导致高达0.71bb的损失。
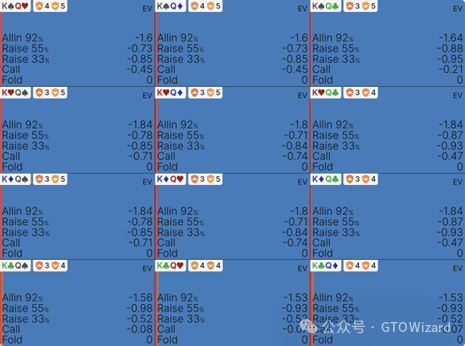
若发现KQs属于跟注范围,很容易自我安慰道”KQo跟注应该也无大碍”,但两者差异实则显著——期望值差距可达0.77BB,即77bb/100手。表面看似相同的牌型,但后门同花潜力极大提升了KQs的价值。
让我们推进牌局:假设UTG以正确范围跟注,转牌发出K♠。此时SB的行动如下:

这张转牌对SB有利,他们仍持有显著的范围优势,因此策略基本保持不变——25%底池下注仍是首选尺度。让我们观察此牌面上不同强度手牌的应对策略。
范围优势并未改变,因此无论手持何种牌型,25%底池下注始终是最优尺度。此时剩余的KJs已接近坚果牌力,但仍倾向选择较小尺度。使用50%与25%底池下注的期望值差异达0.87BB,相当于87bb/100手的决策漏洞。
您应记得在翻牌圈,50%与25%下注尺度的差异为31bb/100手误差,而此刻已扩大近三倍。这本质上是相同的策略错误,但代价却提升至三倍。原因显而易见——转牌圈底池规模大于翻牌圈,但这一提醒仍具价值。
牌局阶段越靠后,决策失误的代价往往越沉重。
终局阶段失误
现在让我们观察当ICM成为重要因素时,决策失误的代价。
在GTO Wizard中分析ICM场景时,期望值不再以BB计量,而是以锦标赛权益百分比呈现。其计算原理是:取牌桌的ICM总值(非全体参赛者),然后将期望值表示为该值的百分比。例如,若牌桌ICM总值为$1,000,某手牌在模拟中的期望值为1,则平均而言该手牌能为我们创造$1,000的1%,即$10的实际货币价值。
在此案例中,我们处于泡沫圈附近,以下是牌桌配置与泡沫系数:
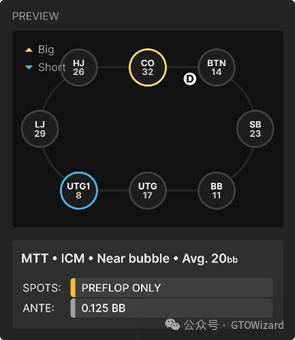
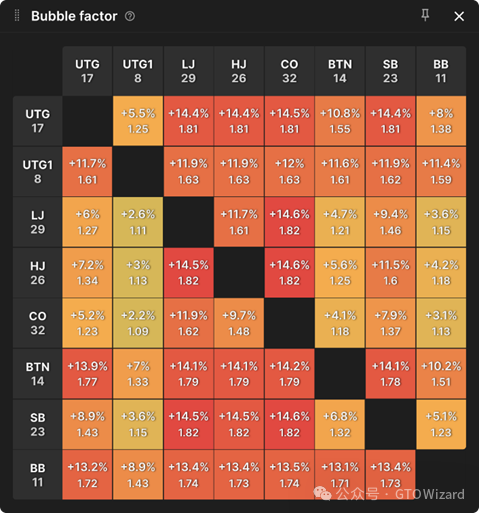
如您所见,UTG1位玩家筹码极短,而BB位也面临出局风险。
当牌局行动弃至UTG1位时,其开池范围如下:
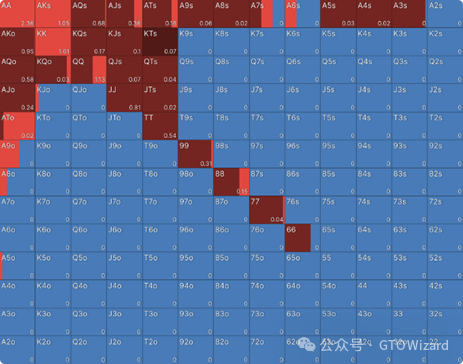
KTs是Kx组别中最后一批全下的手牌,其期望收益如下:
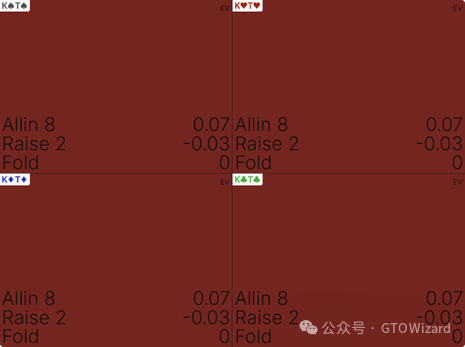
前文我们曾讨论过某些场景下全下无利可图但开池可行的情况,而本例正相反。此处用KTs全下可盈利——能创造0.07%的牌桌权益;但开池将导致0.03%的损失,两者差异达0.1%。这是因为全下往往能直接收池,该手牌本身能阻断大量跟注范围,且被跟注时仍具可观权益。
作为开池手牌则无利可图,因为能对其反加注的范围普遍压制KTs,且若被跟注后未击中翻牌,往往陷入艰难处境。当ICM产生影响时(尤其作为短码),这是至关重要的考量——您最不愿看到的就是投入可观比例的筹码入池后,却要为生存权做出艰难抉择,甚至可能被迫弃牌。此时利用全栈筹码的杠杆效应,将压力转嫁给对手才是上策。
KTs全下可盈利,而K9s则将导致损失:
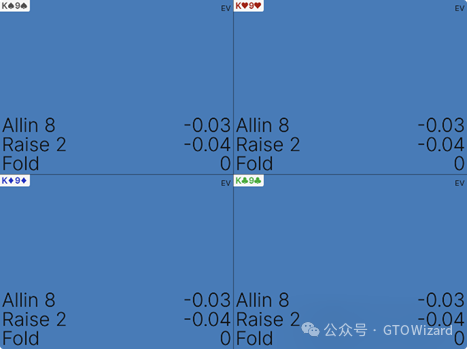
K9s全下将损失0.03%,与KTs的收益差距达0.1%。
假设UTG1以正确范围全下,BB的应对策略如下。需谨记:BB同为短码,若输掉这手牌几乎注定将止步泡沫圈。

AJs是我们未成对跟注范围的底端手牌,其跟注能为我们创造0.38%的牌桌权益。
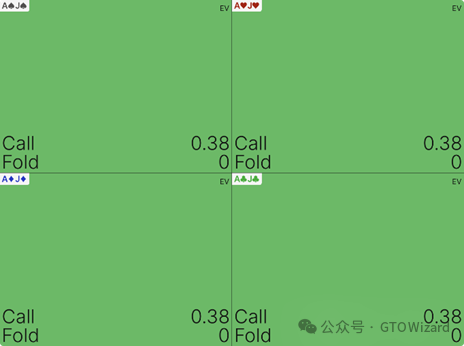
而ATs将导致如下损失:
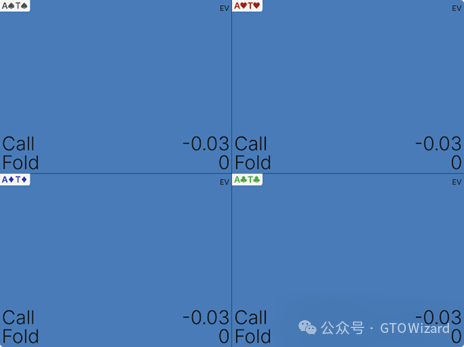
此刻我们观察到两个相近决策间的巨大鸿沟——”正确”跟注与”错误”跟注的差异达0.41%。若偏差扩大两级(例如用A9s跟注),结果如下
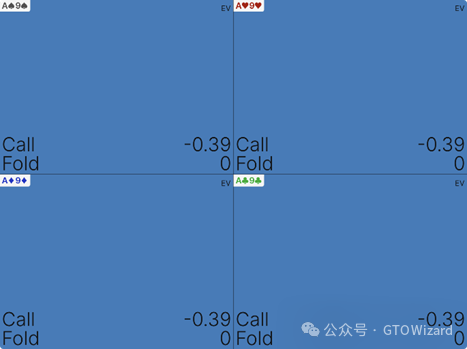
AJs与A9s的期望值差异达0.77%。
这里蕴含着一个重要启示:前例中一级牌力偏差的全下错误代价为0.1%,而用相同筹码量进行一级牌力偏差的跟注错误(如用ATs跟注)代价却达0.41%。错误跟注的成本是错误全下的四倍。
这印证了扑克界的古老格言:”跟注所需牌力强于加注“。错误全下的代价较低,是因为它仍能通过迫使对手弃牌达成战略目标——您可以通过翻前收池或被跟注后胜出两种方式获胜。由于大量弃牌行为的存在,平均底池规模将大幅缩小,使得这类错误的代价相对较小。
错误跟注比错误下注代价更高——因为底池规模必然扩大,且您必须在摊牌时持有最佳手牌方能获胜。
这正是研习ICM至关重要的原因——相同的决策错误会随着赛事进程不断放大。用”仅损失x bb”来合理化错误绝非正确的思考方式,因为失误的真实货币代价远甚于此。
让我们回到以牌桌权益而非BB为单位的计量体系:假设您在11美元周日风暴赛的泡沫圈犯下3%的权益错误,当时牌桌总权益为$200,则实际损失为$0.60,相对于$11的参赛费似乎无足轻重。但若在奖金池约$50,000的决赛桌犯下相同错误,您的权益损失将高达$150——这相当于近14个买入的代价。一个微小的失误,或许只是偏离正确范围一级牌力,却可能让您与巨额财富失之交臂。
扑克学习优先级诊断
今日我们深入探讨了盈利范围底端手牌与其相邻首张非盈利手牌之间的期望值差异。这揭示了若您经常在临界点犯错,将承担的边际错误成本。
l 这也向我们揭示:不同类型决策错误的代价存在显著差异。
l 从技术层面而言,错误弃牌虽不会造成直接损失,却意味着机会成本的流失——若您已投入筹码,这种机会成本尤为巨大。
l 下注失误的后果并不严重,因为即使错误下注仍可能迫使对手弃牌。有时错误全下的代价甚至低于错误下注——因为动用全部筹码的杠杆效应会带来大量弃牌。
l 跟注失误的代价则高昂得多——您无法迫使对手弃牌,必须在摊牌时持有最强牌力,且面对的底池规模往往更为庞大。
l 当ICM成为影响因素时,跟注失误的代价将呈指数级增长——因为错误的真实货币价值会持续累积。若在年度最重要的决赛桌弄错跟注范围,可能导致数十甚至上百个买入的权益损失。
l 下注与跟注失误的代价会随着牌局推进不断叠加。河牌圈的糟糕跟注损失尤为惨重——因为此时底池规模通常远大于前几轮。
在研习翻牌后策略时,这意味着:修正河牌圈失误比转牌圈更重要,修正转牌圈失误又比翻牌圈更重要。这正是GTO Wizard训练功能的价值所在——您能快速识别失误类型及其代价,并零风险专项练习最高成本的决策场景。
这表明在扑克学习中存在低垂果实效应:翻牌前阶段,夯实跟注范围应优先于开池/全下范围的优化——若您正在研习ICM策略则更是如此。掌握跟注范围对于决赛桌与泡沫期至关重要,这些决策可能成为您年度最具价值的资金决策。
核心要点
-
- 若不确定从何入手,请专攻你最严重的漏洞
- 盈利手牌与仅差一级却未入范围的手牌之间,可能存在显著价值差异
- 下注失误的代价远低于跟注失误
-
- 有些手牌适宜下注却不适合跟注,有些适合全下却不适合开池
- 牌局阶段越靠后,决策失误的代价越沉重
- 赛事阶段越深入,决策失误的复利效应越显著
文章来源:GTO WIZARD















评论 ( 0 )