
帕累托法则
帕累托法则(即‘二八法则’)是一项经济学理论——一旦掌握其精髓,您将发现它在包括扑克在内的所有生活场景中普遍存在。
该法则以意大利经济学家维尔弗雷多·帕累托命名,他在20世纪初首次发现这一规律并提出核心主张:
约80%的结果源自20%的成因。
帕累托先生在研究意大利土地所有权时发现了一个有趣规律:约80%的土地被仅20%的人口所拥有。这一发现促使他深入探索该理论,并很快意识到该比例似乎适用于生活与商业的诸多领域。
自此之后,学界观测到无数二八分布案例,例如:
1.
在语言领域中,使用频率最高的20%词汇占据了总出现次数的80%。
2.
微软公司曾公布:Windows与Office系统中80%的系统错误及崩溃源自20%的代码缺陷。
3.在美国,约20%的住院患者消耗了80%的医疗资源
4.80%的污染排放源自20%的工厂。
5.就个人而言,有个例子让我倍感有趣:一位经营餐厅的朋友透露,其75%的餐品销量来自仅占菜单20%的汉堡类选项。
实际分布无需严格符合80/20比例,总和也不必恰好等于100。既存在75/25的分布,亦存在90/10的分布。
在输出结果非路径依赖的领域(即前序行为不影响后续行为),通常不会出现帕累托分布。然而当结果受先前成果影响时,就会出现不均衡分布。
在输出结果非路径依赖的领域(即前序行为不影响后续行为),通常不会出现帕累托分布。然而当结果受先前成果影响时,就会出现不均衡分布。
以财富积累为例:初始资金雄厚者拥有自我教育的资源,从而获得更高收入,而额外财富又可能带来银行优惠利率等正向循环。相反,抛硬币则非路径依赖——每次结果不受前次影响,在大样本下会呈现正态分布。
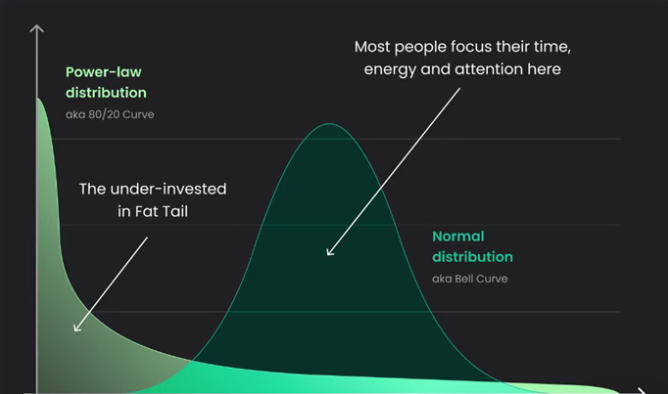
企业高管、思想领袖与励志专家常运用帕累托法则来识别并利用不均衡分布。例如:若企业主发现80%营收源自20%客户群(如中年中产阶级男性),则应投入更多精力针对该群体营销——因为他们已展现消费意愿;若每日80%的工作成果产生于前20%的时间段,就应将核心任务安排在效率最高的清晨时段。
帕累托法则的扑克应用
扑克中存在大量不均衡分布现象。例如:约80%的利润往往来自20%的对手(即娱乐型玩家)。大数据显示,约15%的玩家能实现盈利——这本身就是不均衡分布。其中约5%属于”大赢家”,而顶尖1%的玩家在其级别中赚取巨额收益。这正是不均衡分布中的不均衡分布,再嵌套不均衡分布……
若拥有足够手牌数据库,您会发现大部分利润源自20%的手牌(即游戏中最强的20%起手牌,例如UTG开池范围)。而该范围内前20%的顶级牌力(如JJ+, AJs+, AQo+)将创造其中绝大部分利润。
只需观察GTO Wizard中上述范围的手牌期望值,就能发现其极度不均衡的头部集中特性。前例中AA平均盈利10.05bb,而K8s仅盈利0.01bb。同样,在大型手牌数据库中可见AA是盈利最高的手牌,其次是KK,依此类推——极少数手牌构成了绝大部分利润。
另一可靠的不均衡分布体现在位置盈亏数据上:例如您可能在大盲注和小盲注位置亏损,而BTN位和CO位的盈利很可能占据总收益的主要部分
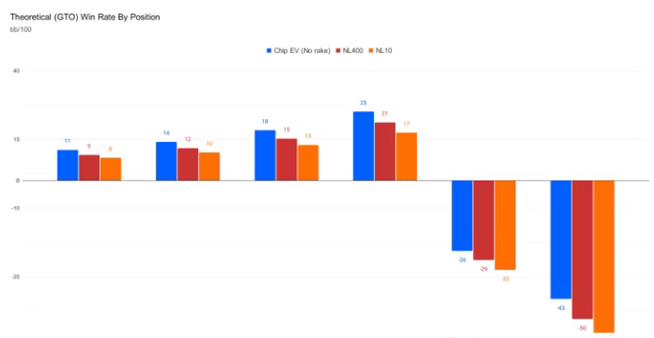
扑克学习中的帕累托分布
帕累托法则让我有机会分享或许是我最钟爱的Tombos21教学视频:
在该视频中,他分享了极具实用价值的”牌局重要性“电子表格。该工具按优先级展示了需要掌握的最关键翻牌后场景,其排序标准综合了出现频率与平均底池规模。
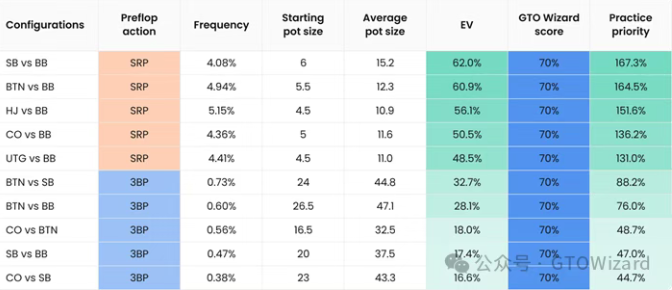
例如,SB vs BB 单次加注底池是扑克中最具价值的场景——因双方始终有资金投入底池,故需优先练习。建议通过GTO Wizard将该场景的掌握度提升至阈值后,再转向下一优先级场景(如BTN vs BB)。
若不确定从何练起,该表格列出的高频场景是最佳起点。人们常倾向于研究前日遭遇bad beat的UTG vs UTG+1 3-bet场景,但此类情形罕见且往往牌力自明。相比之下,掌握在K82翻牌面作为BTN vs BB处理第二对子的技巧更为实用——牌桌会持续出现大量可迁移类似场景。
该表格收录的场景占所有单挑情况的32.74%。
而对抗BB的单次加注底池就占据总单挑场景的22%,且全是表格中的最高优先级。这正呈现帕累托分布:22%的单挑场景构成了最核心的学习领域。
进一步深入:SB vs BB作为首要练习场景,占该SRP对抗BB子集的20%。这正是帕累托分布中的帕累托分布……
因此,您可通过专项训练对抗BB的单次加注底池来利用扑克中的帕累托分布。
马太效应
作为帕累托法则的姊妹理论,马太效应(即累积优势原理)揭示了成功自我强化的规律,这也正是俗语”富者愈富,贫者愈贫”的由来。
该原理得名于《马太福音》25:29:
“凡有的,还要加给他,叫他有余;凡没有的,连他所有的也要夺去。”

马太效应可通过”偏好依附”解释:财富分配倾向于已拥有更多资源的人。现实案例比比皆是——富人常能以低利率借贷,其财富借复利效应持续增长;相反,穷人被视为高风险信贷对象,只能承受高利贷,因深陷债务而遭受负面复利的侵蚀。
更简明的解释是良性循环与恶性循环的博弈。
扑克中的马太效应
扑克中随处可见马太效应的例证:世界顶尖牌手能参与富豪扑克巡回赛——那里娱乐玩家比例更高;顶尖高手甚至受邀参加职业/业余对抗赛(职业与业余选手各占50%)。尽管Triton常客玩家与参加$5000买入赛的职业选手实力差距甚微,但如Stephen Chidwick这类玩家的盈利机会却呈几何级增长。
与此形成鲜明对比的是微级别游戏:由于抽水过高且盈利不足以支撑昂贵培训课程/工具,许多玩家深陷其中难以晋级。
马太效应在游戏机制中同样存在——筹码领先者的ICM优势便是典型体现。
以下三个临近泡沫圈的场景(平均筹码量40bb)将展示UTG筹码深度变化如何影响其开池策略:
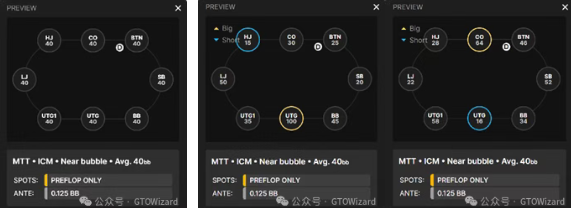
第一种情境:所有玩家均持有40bb筹码。以下是UTG的开池范围:

这同样是平均筹码40bb的临近泡沫圈情境,但UTG持有100bb筹码。

最后一种情境:同样处于平均筹码40bb的临近泡沫圈,但采取对称解法的另一端——UTG作为短码仅持有16bb:

若将全员40bb的范围视作”基准”,可见筹码领先者能盈利游戏的手牌数量显著超越基准——从16.5%跃升至35.8%,较基准范围扩大逾一倍。筹码优势使该玩家能用近似中位的范围在早期位置开池。
反之,短码困境则令UTG仅能游戏7.4%的手牌,不足基准范围的一半。
此非完美例证(因其他玩家筹码深度也会影响策略),但总体而言:锦标赛中筹码孕育更多筹码。
筹码领先者享有累积优势,短码玩家则陷入对等劣势。
结论
帕累托法则揭示:少量投入创造多数产出。
马太效应阐释:优势持续累积,导致少数人占据绝大多数成果。
两大原理的共同内核是产出不均衡性。当单次结果不受前次影响时(如抛硬币),将呈现正态分布;反之,当后续行动受先前结果影响时,必然产生不均衡分布。
扑克中的帕累托法则
从扑克视角来看,帕累托法则清晰揭示了聚焦特定领域的差异化价值。以学习优先级为例:将精力倾注于SB vs BB 单次加注底池而非UTG vs UTG+1 3-bet底池,将产生更显著的能力提升。
扑克中的马太效应
马太效应从多重维度解释了为何少数玩家能实现突破性成功,而多数人始终停滞不前。扑克领域的成功往往自我强化——无论是通往更高级别游戏、更弱竞争环境、优质学习资源、资金支持乃至商业赞助的机会。
若您拥有大型手牌数据库,我强烈建议您亲自探寻其中的帕累托分布。一旦认知此概念,您将发现它无处不在。这犹如在某种程度上窥见了博弈世界的底层代码😎
文章来源:GTO WIZARD















评论 ( 0 )