在策略性扑克游戏中,纳什均衡策略(通常称为 GTO 策略)被广泛视为不可被剥削的策略巅峰。GTO 的核心吸引力在于双人对抗中提供的防御性保障。然而在多人场景下,纳什均衡的基本根基假设不再成立。本文将以纳什距离(Nash Gap)概念为线索,探讨纳什均衡在多人底池中的局限性。
- 多人底池中纳什均衡的缺陷及为何我们仍需追求纳什均衡
玩家的纳什距离定义为:当其他玩家保持策略不变时,该玩家通过单方面偏离当前策略所能获得的最大 EV 提升值。换言之,它量化了当对手策略固定时,玩家通过调整自身策略可获得的收益空间。纳什距离为零表明玩家正针对对手当前策略实施最优应对,意味着对手无法通过单方面调整改善收益。
在双人零和游戏中,纳什均衡概念具有特别良好的特性和吸引力。纳什均衡可以确保:在给定对手策略前提下,双方玩家的策略都是最优的;更重要的是,任何玩家都不会被剥削。由于游戏是零和性质,一方收益即另一方损失。若双方均采用均衡策略,任何偏离都无法提升 EV,也无法被对手利用。因此该均衡提供防御性保障:只要遵循策略,无论对手采取何种行动,都能确保玩家获得最低预期 EV。这使得纳什均衡成为双人零和场景中稳健可靠的理论解。
然而,在多人游戏中,情况存在根本性区别。当玩家采用纳什均衡策略时,他们仅是对其他玩家当前策略的最优应对。但这无法提供像双人零和博弈中的安全性或防剥削保障。
多人底池的核心问题是,多个对手可能同时调整策略。一个在当前策略下最优的决策,当多个玩家同时改变策略时会变得更脆弱。例如在三人游戏中,两名玩家可能(有意或无意)调整策略损害第三人的EV —— 即便第三人正执行最优策略。策缺失略稳定性也就意味着,多人游戏的均衡策略无法像两人零和博弈那样提供防剥削保证。
那么,为什么我们在多人游戏中仍然追求纳什均衡?虽然缺乏防御保证,但在多人游戏中收敛到纳什均衡(或最小化纳什距离)仍能提供宝贵的策略建议。
首先,纳什距离低的策略确保玩家执行近似最优策略,这在实际游戏中往往带来更稳定和可预测的行动模式。事实上,在多数策略学习环境中存在一个合理假设:当玩家不串通、自私地优化自身结果时,系统会自然收敛到纳什均衡这个稳定点。这种均衡的形成源于个体玩家基于自身利益的学习与行动,无需中央协调或玩家间合作。每个玩家改善自身处境的独立行为就足以推动整个系统达到纳什均衡,这在多人动态中具有核心价值。其次,均衡策略可作为学习和制定剥削策略的基准线起点。最后,纳什均衡始终是博弈论的基石概念。它定义了没有玩家存在偏离动机的状态,即便在多人情境中已不具备两人零和博弈的防御属性,其仍然是计算机算法和理论分析的自然目标。
本节将探讨三人 Kuhn 扑克。Kuhn 扑克是扑克的一种高度简化版本,你可能熟悉它作为 “AKQ 游戏”。它最初是两人游戏,其纳什均衡由 Harold W. Kuhn 分析而得名。幸运的是,三人版本中也存在一系列纳什均衡,尽管分析过程比两人版本复杂得多。我们简要回顾一下 D. Szafron、R. Gibson 与 N. Sturtevant 合著的论文《三人Kuhn扑克的参数化纳什均衡族》(收录于 AAMAS 2013 会议论文集,原文链接:https://www.ifaamas.org/Proceedings/aamas2013/docs/p247.pdf)
中所述内容:牌堆仅包含四张牌(A、K、Q、J)。三名玩家各获得一张底牌,且无公共牌。仅设置一轮下注环节:所有玩家需支付 1 单位前注,并选择是否用剩余 1 筹码进行全压。
已知的三人Kuhn 扑克纳什均衡族包含玩家 2 和玩家 3 的自由参数。这意味着存在无限多组均衡解 —— 尽管玩家 1 没有策略选择空间,玩家 2 和 3 仍可在保持自身最优 EV 的前提下调整策略。该均衡族之外是否存在其他均衡仍是未解难题,但我们的 solver 给出了该族内的解。
出现一个有趣现象:玩家 2 可在维持自身 EV 的前提下,选择 0 至 1/4 区间内的参数 β,该参数基本对应玩家 2 的诈唬频率。含 β 的纳什均衡赋予三名玩家的期望值如下所示:
这意味着玩家 2 可以在玩家 1 和玩家 3 之间自由分配特定 EV,即使不存在任何合谋行为。本质上,玩家 2 必须选择参数 β 的取值,若其目标是最大化自身 EV,很可能会根据对手技术水平等观察结果调整该参数。需要强调的是,我们讨论的是理论分析中的简化模型,真实扑克游戏的动态可能有所不同。但理论上,这种特殊现象在三人及以上游戏中始终可能存在。
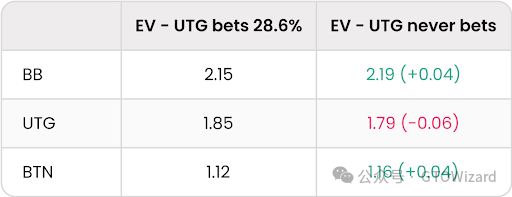
尽管这个案例颇具启发性,但 EV 转移问题在德州扑克中似乎并非主要矛盾。在本文撰写过程中,我们尚未找到在德州扑克多人底池中不影响自己EV情况下在多个对手间转移 EV 的实际案例。观察这种现象在Kuhn 扑克和德州扑克中的区别反而具有教育意义。设想典型三人底池场景:UTG 位翻前公开加注,BTN 位与大盲位跟注,所有玩家过牌至河牌圈。在纳什均衡状态下,UTG 玩家面对过牌时应在河牌圈以 28.6% 频率下注。若强制 UTG 过牌,同时固定 BTN 和大盲位的原始策略,会发生什么?在三人Kuhn 扑克模型中,这将导致 EV 从大盲位流向 BTN 位,而 UTG 的 EV 不受影响。但在德州扑克的案例中,我们观察到截然不同的情况:
此时 UTG 在向 BTN 和 BB 玩家送出 EV!值得注意的是,由于存在抽水,EV 变化总和并不为零。这解释了为何我们认为纳什均衡是稳健策略的核心。在复杂多人底池牌局中,首要任务是打好自己的手牌,实战中捕捉 EV 转移机会往往极为困难。
在本文中,我们探讨了纳什均衡在双人游戏中不可被剥削的保证,为何无法完美迁移到多人场景。理论上,正如三人Kuhn 扑克的例子所示,玩家有时能在不影响自身 EV 的前提下,在对手之间转移 EV。然而,在复杂的德州扑克实战中,这类明确的 EV 转移机会几乎不存在,且极难执行。事实上,纳什均衡提供了一个强大的基准,它能保护你免于犯下昂贵的错误,并引导你在扑克中走向长期成功。
文章来源: GTO WIZARD
















评论 ( 0 )