
坚果听牌作为下注与加注选择具有显而易见的吸引力:它们既能享受弃牌权益,有时甚至能迫使更强手牌弃牌,同时在对手未立即弃牌时仍具备赢取巨额底池的潜力。
然而求解器并不总是激进地游戏坚果听牌。例如在100bb的CO vs BB单次加注底池中,CO在Q♠6♦2♦翻牌面对其坚果同花听牌的持续下注频率仅为69%:
尽管坚果同花听牌进行持续下注优势明显,但求解器并未始终如一地对其下注。
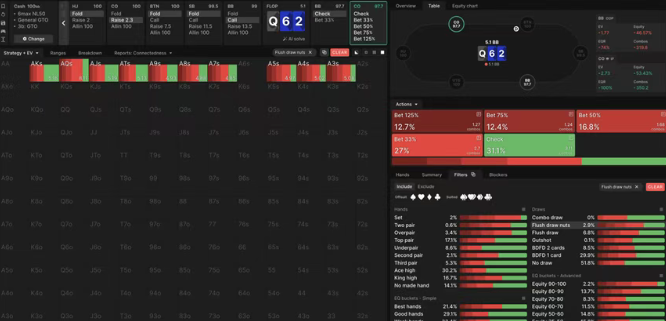
CO的整体持续下注频率(即整个范围而非仅坚果同花听牌的下注频率)在此仅为49%,可见他们游戏坚果同花听牌的激进程度(69%)高于范围平均值。然而这些听牌没有纯下注策略,且当下注时,它们会混合使用全部四种下注尺度。
现象解析
请允许我含蓄地自夸一下,这是我2014年在个人博客上发布的一手牌例。那时我对博弈论、平衡与剥削还知之甚少,但已捕捉到一个重要理念:如果所有人都预期你会用同花听牌持续下注,那么当你未下注时,他们便不会认为你在转牌击中了同花。这使你有动机过牌部分同花听牌,从而利用他们的怀疑获利。
由于这手牌来自已过时的”Ante Up”赛制,牌局历史可能较难理解。但简而言之:我作为翻前加注的有利位置玩家,手持A♦T♦在Q♣4♦2♦翻牌面选择过牌,并在5♦转牌击中同花。对手再次过牌后,我下注,遭遇加注(剩余筹码约一个底池大小),我选择跟注。河牌5♠发出后对手全下,亮出K♠J♦——最终在毫无胜算的情况下投入了约四倍底池的资金
正如我在博文中所写:“当你在翻牌圈过牌后,仍能在转牌圈组成同花,这种能力极具价值。“
这里体现了扑克策略的深层原则:限制自身范围是危险的。当对手能轻松持有坚果牌,且准确预判你极少拥有坚果组合时,他们便可用极化范围进行大额下注,将你最强的牌力贬为纯粹的抓诈牌。有效筹码越深,这种危险系数越高。
这并非铁律。你无需因担忧牌堆底牌在转牌与河牌组成公对而自己范围内毫无四条的可能性,就扭曲翻牌圈策略。但对于常见场景(如转牌发出第三张同花),求解器通常会通过将坚果听牌分散到所有行动中来提前布局。
当然,求解器并非在”未雨绸缪”——它们根本不会”思考”(据我们所知)。它们通过响应激励机制、修补可被利用的漏洞来实现期望值最大化。若求解器将某手牌混合于多个行动中,则该手牌在所有行动中必然具备相同的均衡期望值。这意味着如果你在此场景中对所有坚果同花听牌都下注,对手就能通过某种方式加以利用(很可能就是在你不可能持有坚果牌的游戏树分支上进行前述的大额下注),这种威胁正是激励你偶尔在这些分支中亮出坚果牌的原因。
实验验证!
我们可以通过节点锁定来测试并探索这一理念。为此需要创建自定义解决方案。同时让我们简化决策树——既然我们更关注是否下注而非下注尺度。当只允许单一尺度的下注时,CO在Q62tt牌面的整体持续下注频率为70%,但其坚果同花听牌的下注频率达76%,这再次证明此类听牌确实是优于平均水平的候选下注牌型:
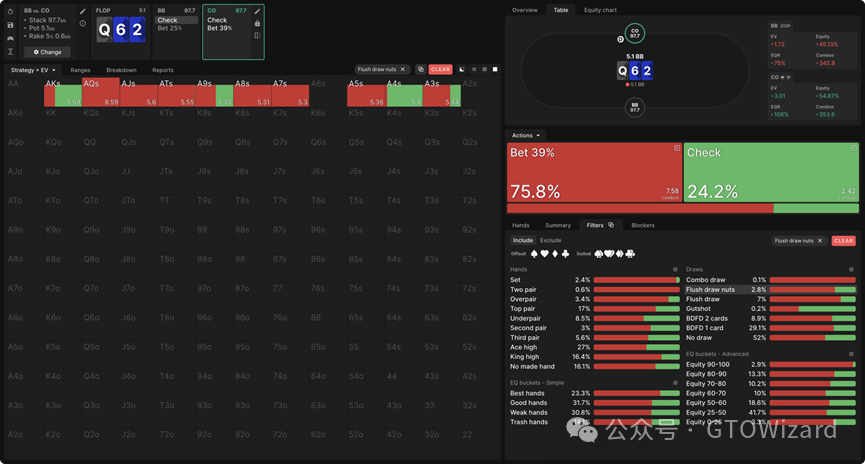
求解器确实展现出对某些组合下注的偏好,尽管偏好程度不强。例如A♦8♦作为纯下注策略时表现更优,收益高出6bb/100;而A♦3♦无论下注或过牌期望值相同,因此采用混合策略。

A♦9♦是均衡状态下混合较多过牌比例的坚果同花听牌组合之一。但若我们将CO的策略锁定为纯下注A♦9♦,他们会通过增加其他混合策略组合(AK、AT、A4和A3)的过牌频率来进行补偿。
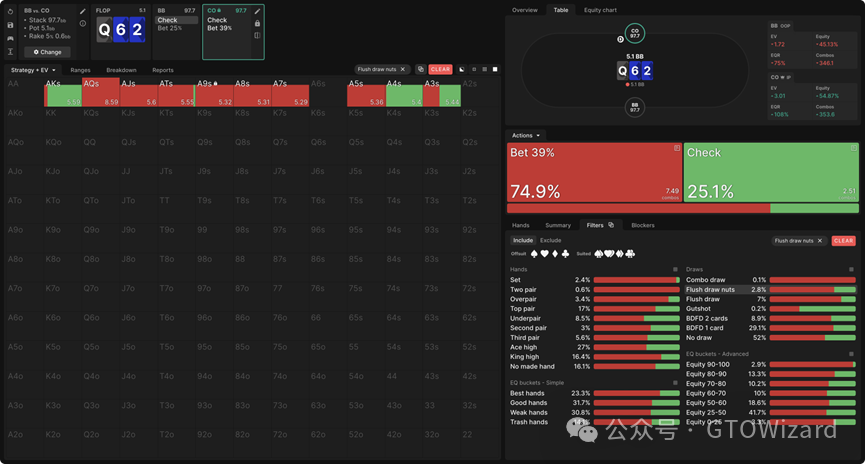
若将A♦9♦、A♦T♦和A♦4♦锁定为纯下注,则原本在均衡状态下为纯下注的A♦7♦和A♦5♦会开始混合部分过牌进行补偿:
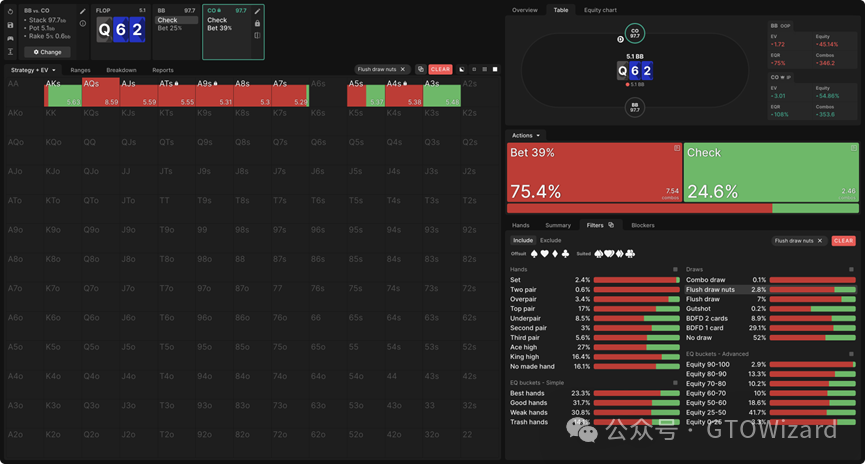
请注意:即使我们为CO的下注策略引入更多固定规则,其过牌频率仍保持相对稳定。事实上,尽管被迫以”次优”方式游戏越来越多组合,他们的期望值依然维持不变。
在游戏树的每个分支上保持合适的坚果听牌频率,远比对特定组合采取特定行动更重要。
求解器偏好下注某些组合确有缘由,但除兼具顶对的A♦Q♦外,这些原因并不关键。某个组合可能少阻断BB的弃牌范围,或具备稍好的对子补牌。当拥有双核处理器的算力时,CO大可将这些细微差异作为决定下注与过牌组合的决胜因素。但这些仅是决胜因素,您选择具体组合下注的方式并不十分重要。
核心结论是:CO的均衡策略会在其下注与过牌范围中均包含部分坚果同花听牌,而在每个范围内保持适当的坚果听牌频率远比用特定组合执行特定操作更重要。计算机能做出极其精确的区分,但作为人类,您可采用启发式方法(例如下注高踢脚牌、过牌低踢脚牌),甚至随机化处理——比如用所有组合进行25%频率的过牌。

筛选功能使用指南
这一原则适用于CO存在显著过牌范围的任何翻牌面。但我特意选择Q62牌面,是因为CO在此的坚果同花听牌均非组合听牌。在QT2这类翻牌面,”坚果同花听牌”筛选器将不会包含A♦K♦和A♦J♦。虽然添加组合听牌筛选器能捕捉它们,但也会同时纳入K♦J♦等非坚果组合听牌。使用筛选器时务必谨慎,确保精准捕捉目标组合。
同花成牌(方块)转牌的策略
翻牌圈过牌通过后的策略
以下报告展示了CO过牌后,BB在所有转牌圈的下注策略。请注意:在均衡状态下,方块转牌被大尺度下注的频率最低: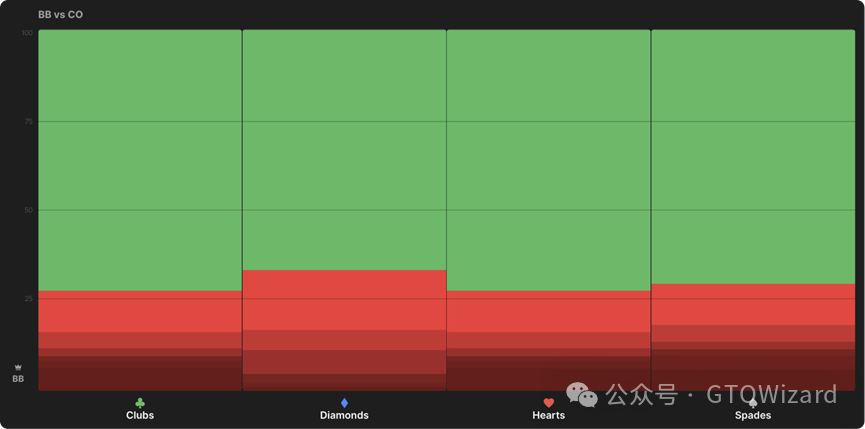
虽然无法对自定义解决方案生成报告,但我们可以选择8♦这类看似无害的方块牌,通过策略对比观察因CO在翻牌圈更多下注同花听牌引发的变化。
我们还需稍调整自定义解决方案的参数——因为我们的假设是:当CO限制自身范围时,超池下注将在BB的策略中扮演更重要角色。我并未自动生成所有下注尺度,而是为双方玩家设定了转牌与河牌圈的固定下注选项:25%、67%或200%底池。
在8♦转牌面,BB的均衡策略并未包含太多超池下注:

当CO被锁定在翻牌圈下注全部坚果同花听牌时,若其未进行下注,则BB在转牌圈的大额下注将更具吸引力:

需注意:在此场景中CO仍持有同花牌型——他们通过过牌更多低端同花听牌来补偿全下坚果听牌的策略。因此尽管CO范围内包含不少同花成牌,BB仍可通过超池下注进行剥削。
当CO被迫在翻牌圈下注全部同花听牌时,若其在翻牌圈过牌,BB就能在同花完成的转牌面对其施加巨大压力

结论
在翻牌圈对同花听牌采用纯下注策略未必是糟糕选择。事实上,面对不频繁使用过牌-加注的对手,即使均衡策略包含大量过牌,采用全范围持续下注也可能是正确的。但这终究是一种策略选择,您应以清醒的认知看待其中的风险与回报。
对手将如何利用您的选择?您认为他们是否会真正实施这些剥削策略?他们是否会过度倾向剥削,从而激励您反向调整并进行反剥削,正如我在2014年所做的那样?
对均衡解决方案理解越深入——不仅知其然,更知其所以然——您就越能识别牌桌上的选项,并针对特定对手选择最优策略。
文章来源:GTO WIZARD















评论 ( 0 )