一个更为现实的例子
没有其他任何信息,这里会随机出现一张黑桃牌的概率至少在35%,1-(38/47)(37/46)=0.35。
但是,从对手的打法来看,我们认为他可能有一张弱黑桃牌。从我们的打法来看,对手正确地推断出了我们有一张强黑桃牌的概率为20%,弱黑桃牌的概率为80%。也就是说我们领跑的概率为20%,那么我们的策略应该是什么样的?
很明显,当我们击中强同花牌组时绝不能跟着过牌。我们也真的无法改变自己的下注尺度,因为我们剩余的筹码量低于当前底池尺度。这说明我们仅有的选择就是判断这手无法对手的手牌应该全压的频率。如果我们每一次都做这个决定,对手就能够准确地跟注我们所有的下注。这使得我们在持有一张强黑桃牌时的期望值为-$200,(0.2)($2000)-$600=-$200。
如果我们只用强同花牌组下注全压,对手就会一直弃牌,我们赢得$800底池的概率为20%,EV为$160,(0.2)($800)=$160。
为了找到最佳诈唬频率,我们首先需要制定出一个对手期望值的公式。当我们下注的时候,他唯一的选择就是弃牌或跟注。弃牌的期望值是零。跟注的期望值公式如下:
EV跟注=(P赢率)($1400)+(1-P赢率)(-600)
EV跟注=(P赢率)($2000)-$600
当我们绝不诈唬时对手的赢率就是零,如果我们一直诈唬(因为我们拿到最佳牌的概率为20%),那么对手的赢率就是80%。令S为我们的诈唬频率(即我们无法赢牌时下注的概率)。注意此时我们下注的总概率为P下注=(S)(0.8)+(1)(0.2),那么对手赢牌的概率就是P赢牌=[(S)(0.8)]/P下注=[(S)(0.8)]/[(S)(0.8)+(1)(0.2)]。
下图呈现了我们的诈唬频率和当我们下注时对手赢牌概率之间的关系。
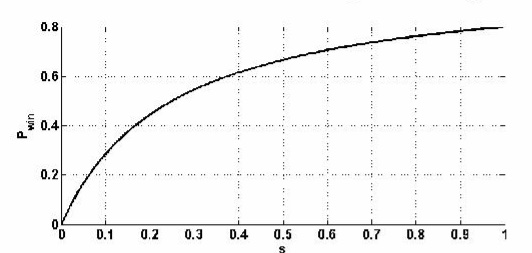
由于我们并不希望对手剥削我们,所以我们要采取最佳诈唬频率。也就是让对手EV跟注=EV弃牌=零的频率。全压时我们的S为10.7%。
EV跟注=($2000)[(S)(0.8)]/[(S)(0.8)+(1)(0.2)]-$600
S=0.107。
这说明当我们错过同花成牌时(概率为80%),我们用非同花手牌下注的概率为10.7%,那么跟着过牌的概率就是89.3%。如果我们诈唬过于频繁,从理论上来说对手跟注时我们会输钱;如果我们降低诈唬频率,我们会错过有利可图的诈唬机会,当我们下注时对手会弃牌,他们知道我们的手牌是强牌。
对手过牌之后的总期望值等于我们跟着过牌并输牌时的底池尺度。当我们下注时,对手跟注的期望值就是零,(0.8)(1-0.107)($600)=$571.43。
就算对手有80%的摊牌权益,在我们的诈唬策略之下他也只有71%的权益,$571.43/$800=0.17。
针对一个常规的诈唬频率,如果对手剥削我们的错误,那么期望值就是:
EV对手=P下注[(EV跟注,EV弃牌)最大]+(1-P下注)($800)
我们根据公式绘制出了下面这张图表:

通过图表我们确实发现对手最低期望值是S=10.7%的时候。在这个例子中我们也能发现有一个点的情况几乎是对称的:低于这个点和高于这个点都存在一个相同的期望值。
(注意:正如David Sklansky在他《扑克的理论》一书中解释的那样,获得同样结果的第二种方式就是注意观察对手赔率在14-6的时候,必须是你价值下注与诈唬的比率。14-6和20-8.6是一样的。所以你全部手牌中有8.6%是可以诈唬的,也就是80%中的10.7%。)
游戏近纳什均衡策略
我们第一个诈唬的公共牌面为6♦️5♥️4♠️7♦️8♠️,我们发现一个无关紧要的下注尺度是底池尺度的2.4倍。如果我们下注这个尺度,那么对手的弃牌期望值和跟注期望值就是零。我们还发现如果下注额度高于这个值,对手每次都会直接弃牌。这并没有改变我们的期望值。
但是,如果我们下注高于底池的2.4倍并且对手有时候会无意中跟注我们,那么我们就会比只下注2.4倍底池投入更多的钱。即使在对手实施最佳打法时我们下注2.4倍底池尺度的期望值等于高于这个尺度的时候,更高额的下注给予了对手更多犯错的机会。
在第二手牌中,公共牌为J♦️T♠️4♠️K♠️3♠️,在不进行剥削的情况下我们无法改变自己的最佳诈唬频率。再回顾对手的整体EV图表时,我们看见了对称部分符合纳什均衡。
这就说明我们下注过高或过低都会损失同样的权益,前提是对手的采取了最佳打法。这里,相比较其他与纳什均衡毫无相关的打法反而是最安全的。但是,如果我们真的很不擅长遵循这个下注策略,最终我们的诈唬频率要么是零要么是40%。
在最差的情况下,我们下注频率低于最佳频率,我们下注率为零的时候,对手获得的期望值就是$640;在最差的情况下,如果我们下注频率高于最佳频率,我们下注率为100%的时候,对手的期望值就是$1000。所以如果我们非常不擅长把控最佳下注频率,我们就该瞄准期望值较低的那个,因为我们下风期的错误是有下限的。
在更为复杂的手牌中,若我们决定下注,对手会有更多的选择(不仅仅只有跟注或弃牌),高于纳什均衡的下注频率通常比低于纳什均衡的频率糟糕,因为频繁的下注给了对手更多额外的选择:他能够决定自己是跟注还是加注以此来提升底池的尺度。






评论 ( 0 )