《解析无限德州扑克》第六部分 各类主题（1）

还有一个关于线上扑克的讨论，内容包括跟踪程序和单挑手牌数据最重要的特征，以及多桌牌况和牌桌选择。

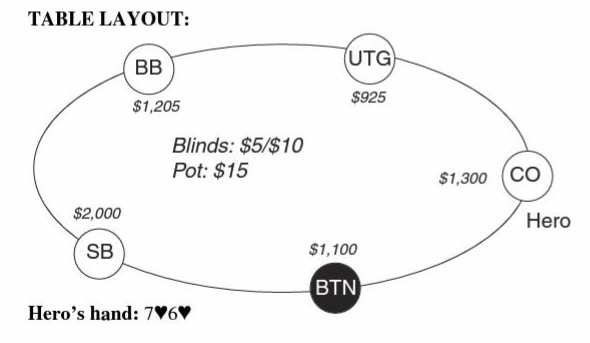
你的底牌：7♥️6♥️

行动：第一位玩家弃牌。你加注到$35,后面两名玩家弃牌，大盲位玩家跟注。此时底池$75。

翻牌：两名玩家过牌。

转牌：8♥️

行动：大盲位玩家下注$65，你跟注。此时底池额度$205。

河牌：3♠️

行动：大盲位玩家过牌，你下注$150。

任何一名理智的玩家在这里都会用有摊牌价值的手牌跟注我们的下注。因为我们几乎会游戏任何各类具有些许价值的手牌：

l 如果我们有一张A牌，我们会下注翻牌圈。

l 如果我们有一张K牌或任何具有摊牌价值的弱手牌，我们都不会下注河牌圈。

l 如果我们翻牌圈击中暗三条，我们会下注翻牌圈或加注转牌圈来对抗对手的听牌。

l 如果我们在转牌圈击中三条8，我们就会在这个转牌圈加注。

l 如果我们的底牌是3-X，我们会弃牌于转牌圈。

所以，我们可能拿到的唯一价值手牌会是K-X、8-9或一些A-3。另外，我们的整体范围在这个河牌圈是非常大的，因为我们可以用很多听牌跟注这张转牌。这会使得我们的手牌没有价值（一组废听牌），所以对手可能就会用任何对子跟注，从而出现一次糟糕的诈唬。

判断一个诈唬是否有利可图存在多个同步的因素：

l 我们拿到一手强牌的概率（从对手角度而言）。

l 对手会用于跟注我们手牌的概率。

l 相对于底池尺度的下注尺度。

l 诈唬频率。

本章节我们的目标是找出这四个因素直接的确切关系。

实际上，如果我们的筹码量足够多，我们的权益就是整个底池。一般而言，我们期望拿下整个底池！这很显而易见，因为我们真的可以全压每一手牌。如果我们有一张9且筹码量足够多，那么对手的跟注就是无利可图的。

结果就是对手每次都会弃牌，我们拿下整个底池。

我们也可以通过计算精确“漠不关心”的下注尺度来回答这个问题。换言之就是我们下注后无所谓对手是跟注还是弃牌。由于弃牌的期望值始终都是零，所以我们希望对手针对我们行动的跟注期望值也是零。

如果我们的下注尺度低于这个数量，对手的跟注就会是有利可图的。如果我们下注高于这个数量，对手跟注的期望值就会是负的，所以每一次对手都会弃牌。但如果我们有可能输掉这手牌，下注尺度高于漠不关心的尺度就会导致对手的行动有利可图，但在这里再差我们还可以分割底池。

令eq为我们有一张9的概率。那么，对手跟注一个下注尺度的期望值就是：

EV跟注=（1-eq）（底池尺度/2+下注尺度）-下注尺度

在不失一般性的情况下，我们可以将底池尺度调整到$1，然后除以同样的下注尺度，那么就得到这个公式：

下注尺度新=下注尺度/底池尺度

此时我们用1代表底池尺度，以及我们的下注尺度和底池下注尺度的比率。这改变了对手EV的公式，此时他的EV呈现出了当前底池尺度很小的一部分。

EV跟注=（1-eq）（1/2+下注尺度）-下注尺度

根据上面设定，他弃牌的期望值为零，EV弃牌=0

继续我们的分析，这里的打法（只针对你有一张9的时候）是你一直会用一定的数量下注河牌圈，从长远来看你并不在乎对手的策略是什么。因此，你希望对手的两种选项都具有同样的期望值。所以，我们全压时就可以得出下面公式：

EV弃牌=EV跟注

0=（1-eq）（1/2+下注尺度）-下注尺度

下注尺度=（1-eq）（1/2+下注尺度）

下注尺度=1/2+下注尺度-（1/2）（eq）-下注尺度（eq）

下注尺度（eq）=1/2-（1/2）（eq）=（1/2）（1/eq-1）

这意味着如果我们根据这个公式衡量我们的下注尺度，那么从长远来看我们不会关心对手的策略。也就是说对于对手来说他们的期望值为零时，进行同样的跟注当他们弃牌时我们的期望值就是整个底池！

若用图表描绘出这个公式，那么我们就会得到下面这张图：

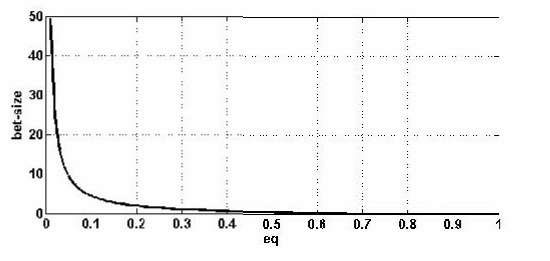
如果我们拿到一手随机牌，我们有可能拿到一张9（我们知道对手没有9），那么这个可能就是17.2%。

0.172=1-（41/45）（40/44）

面对这个公式，我们可以得出最佳下注尺度为2.4。

2.4=（1/2）（1/（17/99）-1）

由于我们将下注尺度定义为我们的下注尺度与底池的比率，所以当对手的跟注期望值为零的时候我们的下注尺度始终都是底池的2.4倍。

遗憾的是，我们的筹码量不会总是多到足以进行这个倍数的下注。如果下注过于小额，你会给对手非常好的赔率来跟注，那么对手的跟注EV就会变成正的。比如，如果底池尺度为$500，我们剩下$750，我们就只能跟注底池额度的1.5倍，$750/$500=1.5。

那么此时对手的期望值就是0.1566，（1-17/99）（1/2+1.5）-1.5=0.1566。

记住这个期望值也可以用$/底池来表达，所以我们可以通过用底池额度乘以这个比率来计算对手确切的期望值，（0.1566）（$500）=$78.3。

正如大家所见，底池越大，我们下注的倍数就越小。也就说明对手的跟注期望值会越高。从另一方面而言，如果我们下注过于大额，比如底池的6倍，我们可以计算出对手的跟注期望值是负的。

（1-17/99）（1/2+6）-6=-0.616

所以在一个$500的底池中，跟注会引起对手的期望值为-$308.08。

于对手来说幸运的是，他可以直接弃牌，弃牌的期望值为零。

如果我们的下注尺度始终高于“漠不关心”的尺度，优秀的对手会一直弃牌，并且我们总是可以赢得底池。但差劲的玩家可能会时不时的跟注，并非是出于对你的不信任，是因为根据公式的结果我们不得不下注，跟注的期望值于对手来说是负的，我们会赢到钱。

另一方面，如果我们的下注尺度小于公式给出的结果，对手跟注的期望值就会是正的。只有对手每次弃牌时我们才会有好的表现（因为他的期望值为零），我们并不介意对手犯弃牌的错误。

所以在这种情况下，最好下注的尺度高于计算出的漠不关心尺度，这样可以最大化对手犯错的概率。在其他情况中（比如对手可能持有好牌的情况），下注高于公式计算出的结果其实是个错误。

总结，从案例手牌中我们得到的重点就是在我们可能拿到的手牌中我们应该如何选择下注尺度。另外，在这个牌况中，对手至少是可以参与分池的，但有时候会输牌于你更好的手牌，你越有可能拿到好牌，你就越不该下注，你拿到好牌的概率越低，你就越该下注。