学习是扑克职业选手工作中不可或缺的一部分,同样地,对于任何希望提高的德州扑克爱好者来说,学习也应该是必不可少的。
那么,扑克职业选手是如何学习的呢?让我们通过Gabriele ‘KingMavE911’ Re的分析来一探究竟。

这位扑克选手将焦点放在了2023年11月的9人桌Spicy 50赛事中的一个关键时刻。在这个场景中,主角需要决定在底池中剩余3.5个大盲的情况下,如何应对来自中间位置的第二位玩家的加注和小盲的10.5个大盲的全下。
第一步:估算初始加注者的范围
Gabriele首先估算第一个发言玩家的范围。他通常使用HRC软件进行学习,输入了比赛的奖金分配、记分牌量和位置信息。
根据平衡理论,程序返回了一个17%的开池范围:
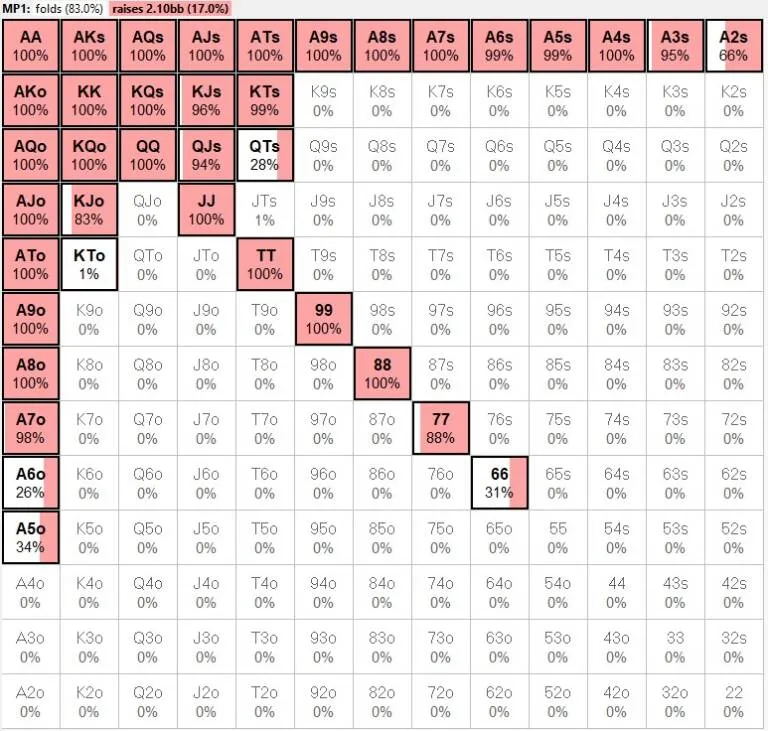
Gabriele随后根据他对比赛对手的了解手动调整了范围
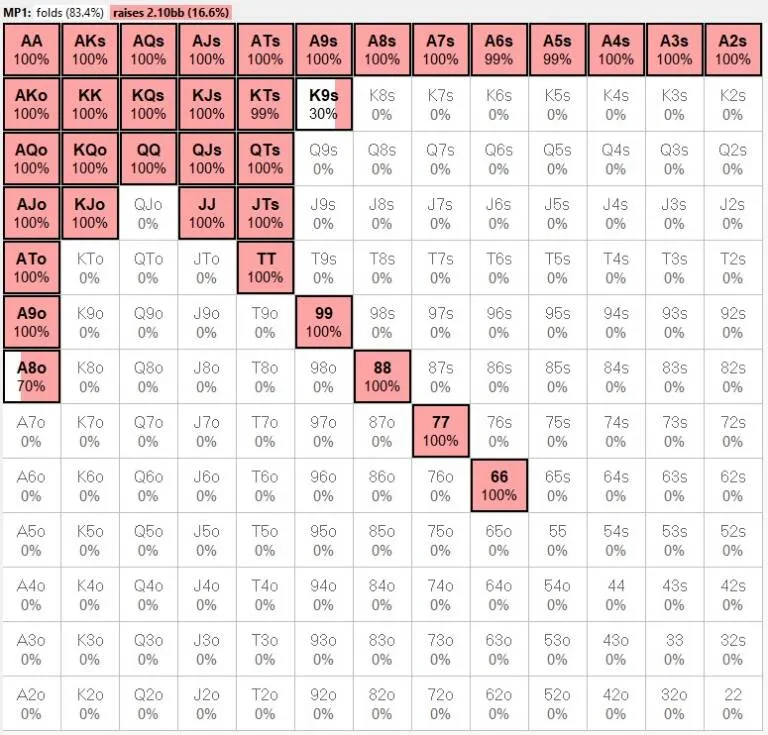
我调整了初始加注者的范围,频率上降低了0.5%,几乎可以忽略不计,但范围的组成明显不同:理论上的范围偏向于非同花的A-x组合,例如很少开池的同花非连张牌。实际上,我认为人们还没有完全接受这个概念,即在决赛桌的这种深度下,A7o这样的牌比QTs更好,因此我预计他们的开池范围会有所不同。
第二步:估算全下者的范围
接下来,需要评估小盲全下10.5个大盲的范围。软件根据分配给初始加注者的范围返回了一个8.9%的范围,具体组合如下:
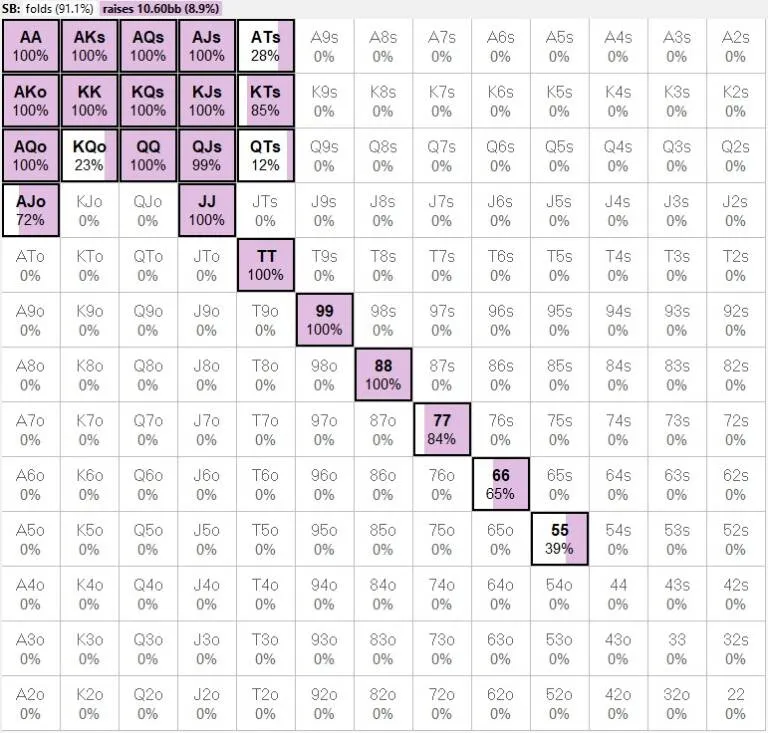
Gabriele也进行了调整
最初我调整了小盲的范围,但频率基本保持与理论范围一致。实际上,我更换了一些组合,用我认为对手更可能采用的组合替换了理论上的组合。
Gabriele调整后的范围如下
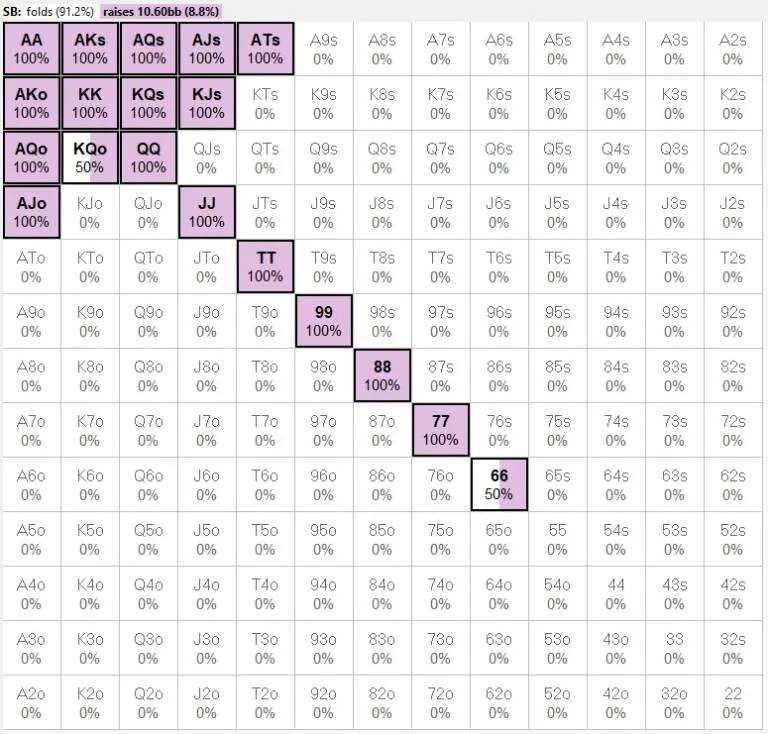
第三步:检查输出结果
接下来,通常需要拿出纸、笔和计算器来计算大盲的期望值,但如今这类工作通常由程序完成。
根据HRC,大盲的理论跟注范围——即程序自动分配的范围,由15.1%的牌组成:
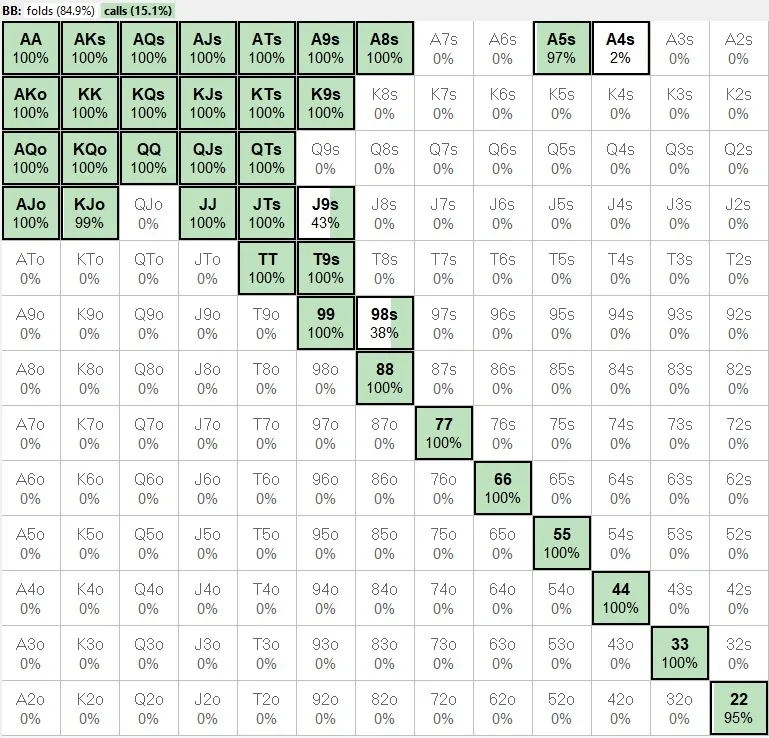
使用Gabriele手动调整后的初始加注者和小盲的范围,大盲的跟注范围变为以下:
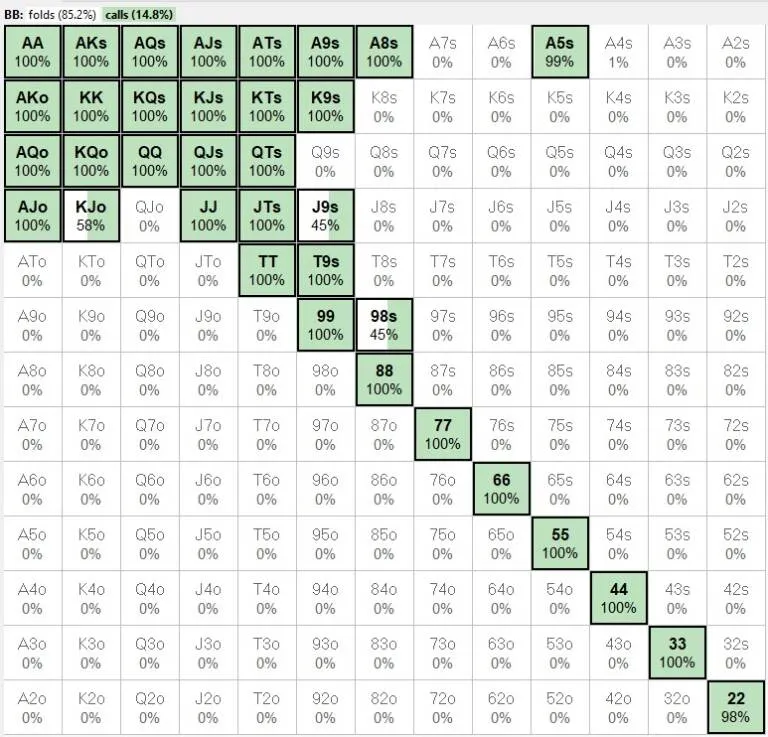
从表中可以看出,AJ是明显的跟注牌,实际上在软件用默认数据生成的表中也是如此。但到底有多明显呢?
从软件返回的跟注范围表中,Gabriele还提取了正期望值:如图所示,AJ的正期望值为+0.1,在ICM中,这位扑克选手表示这是“不可忽视的”。
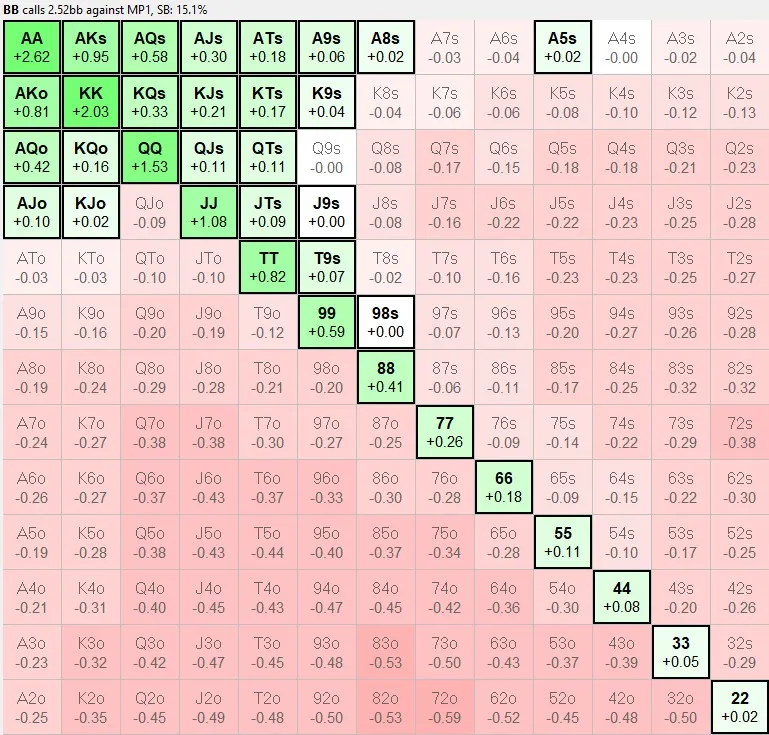
第四步:调整场景
为了更深入地分析这个关键时刻,Gabriele进一步手动调整了小盲的全下范围,针对调整后的初始加注者范围。
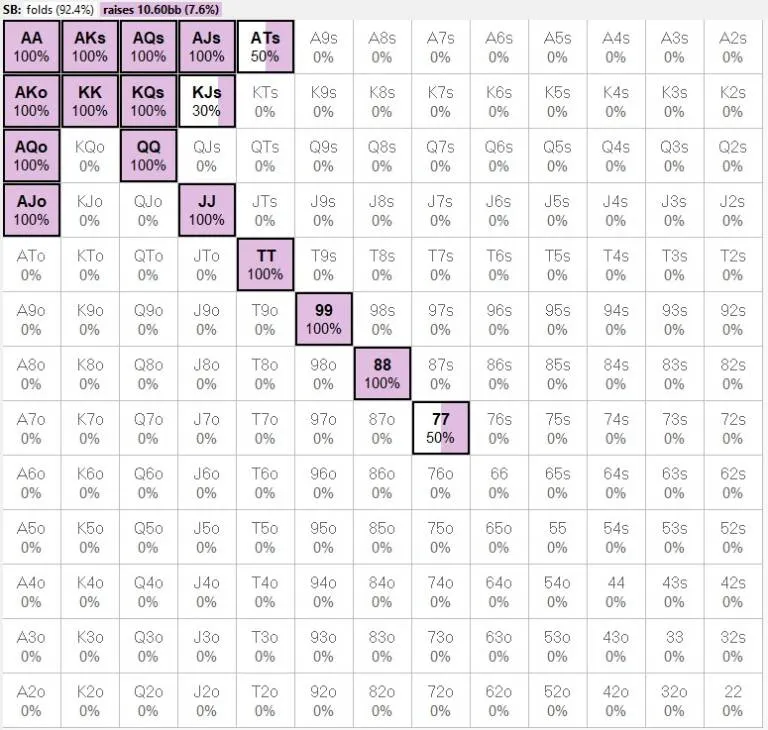
在这种情况下,大盲的跟注范围大幅缩小:AJ的正期望值减少了十倍,从0.1降至0.01!
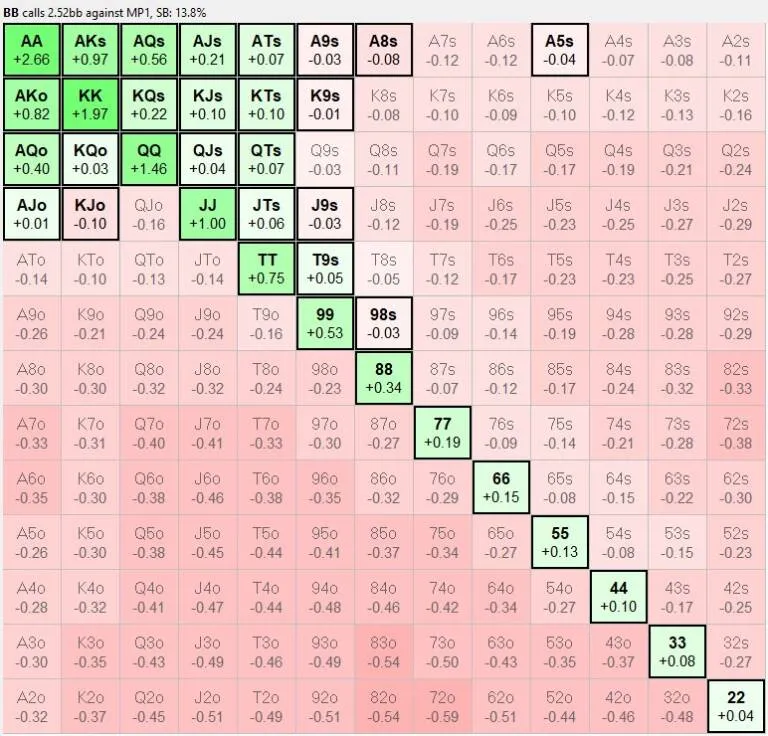
如图所示,这里AJ的正期望值为+0.01,因此从数值上看,这是一个值得考虑的点,但选择如此边缘的点是风险较高的,因为只要其中一个范围稍有变化,我们的期望值也会随之改变:例如,如果初始加注者决定不开池A3s而是弃牌,我们的再加注就已变为负期望值。
结论
最初,Gabriele认为用AJ跟注是理所当然的,但经过分析后,他意识到这个关键时刻比最初感知的要复杂得多:
我为小盲分配的第二个范围非常紧,但在现实中也可能是合理的,实际上AJ可能真的更倾向于弃牌而不是跟注。从分析中可以看出,随着范围的变化,我们的实际应对策略也会发生多大变化。在第一个例子中,AJ的正期望值为不可忽视的0.1,而在第二个例子中则变为可以忽略的0.01。在两个例子之间,我们很可能在现实中更多地面对实际的而非理论上的情况,因此,那些因为认为从理论上是明显的跟注而放心跟注的人,比如我在游戏中代替主角时所做的那样,在现实中可能会面临一个非常边缘甚至负期望值的局面。
文章来源:扑克档案室















评论 ( 0 )