如何精准打牌2 第一章：杠杆作用

相反，被压缩范围中的中等牌力牌型就会因为杠杆作用输掉价值。如果要冒险在河牌圈作出另一个艰难决策，那么在转牌圈跟注就没 那么有利可图了。

尽管一手牌开局的时候最重要，但是关于后面回合下注的考量甚至 会影响到河牌圈决策。在最佳扑克策略中，我们发现如果把加注引 入到A到5游戏（Ace-to-Five Game）中，两位玩家的平衡策略都会降低下注频率。如果你要冒着被两极化范围加注的风险，那么薄价 值下注就没那么有吸引力了，因为你的牌型可能会变成抓诈唬牌。

本章结束时，你应该可以：

♠ 了解后面回合下注的可能性如何影响前面回合的下注和跟注决策。

♠ 用杠杆作用在前面回合生成额外的弃牌胜率。

♠ 在不同回合用两极化范围下注时估算不可剥削诈唬频率。

♠ 制定前面回合的下注尺度时提前计划。

♠ 制定使得对手对于不同的诈唬策略不偏不倚的跟注策略。

有两个下注回合，但是牌型价值不会变。第一个下注回合是“转牌 圈”，Opal总是过牌。我们不会给她下注或加注的选择，因为我们 已经知道她在平衡情况下不会选择这两个行动。Ivan可能会过牌或者下注，下注尺度在$1-$3之间。

面对下注的时候，Opal可能会跟注或弃牌。如果她跟注了小于全压 的下注，然后在“河牌圈”再次过牌，Ivan可能会过牌或者用任意尺度下注。Opal可能跟注或者弃牌。如果走到摊牌，那么牌力更高 的牌型会胜出。

1.有了这个额外的下注机会之后，Ivan的期望值会提高，降低还是不变？

2.Ivan在每个回合的最佳下注尺度是什么？

3.Ivan拿着A的时候会在转牌圈过牌吗？

4.Ivan拿着Q的时候在转牌圈的下注频率会比河牌圈的高还是低还是 一样呢？

5.Opal在转牌圈的跟注频率会比河牌圈跟注频率高还是低还是一样呢？

6.假设下了前注之后有效筹码量是$24。Ivan在转牌圈的下注尺度应 该是多少？下注范围是什么？

在回答下面的问题时，我们会更详细地解释为什么这是正确的，但 归根结底还是杠杆作用。用两极化范围进行的转牌圈下注能得到额 外收益，因为它背后有河牌圈下注的威胁在支撑。Ivan可以通过在河牌圈用两极化范围下注盈利，所以组成河牌圈下注范围的牌型在 转牌圈被跟注的时候有额外价值。

2.Ivan在每个回合的最佳下注尺度是什么？

计算最佳下注尺度是很复杂的数学运算，所以我直接给出结论，方 案是在两个回合都用底池大小的相同比例下注。在这个情形中，这意味着两次下注尺度都是底池的一半：在转牌圈下注$1到大小为$2  的底池，在河牌圈下注$2到大小为$4的底池。如果有效筹码量是$8，那么Ivan就会在两个回合都采用底池大小下注——在转牌圈下注$2到大小为$2的底池，在河牌圈下注$6到$6的底池。

这称作底池的几何增长（geometric growth of the pot），在处理两极化范围的时候这个是重要的概念。  不管有多少个下注回合，拿着完美两极化范围的玩家的最佳策略是在每个回合都用底池大小的相同比例下注，使得最后一次下注是全压。

“完美两极化”意思是他只用胜率为100%或者0%的牌型下注，例 如这个例子中的A和Q。一旦引入了听牌和牌型价值改变的可能性， 下注尺度就会变得更复杂，但杠杆作用的概念依然适用。

3.Ivan拿着A的时候会在转牌圈过牌吗？

不会。Ivan拿着A的时候目标是往底池投$3。现在有两次下注机 会，他就有很多办法可以做到这一点。他可以在转牌圈下注$1，在河牌圈下注$2，或者在转牌圈下注$1.01，在河牌圈下注$1.99，或者在转牌圈不下注，在河牌圈下注$3，等等。

但是他不会对这些选择不偏不倚。即使Opal对每个下注策略的应对 策略都尽可能好，底池的几何增长依然是可以让Ivan赢到最多钱的策略，所以他每次都会选择这个策略。

Ivan拿着A的时候不需要通过在转牌圈过牌去欺骗对手。即使Opal知 道他拿着A的时候一定会在转牌圈下注，她也什么都做不了。她不能在转牌圈弃掉所有的K，因为这样的话Ivan会诈唬。如果转牌圈 被过牌通过，她无法在河牌圈盈利，即使她确定Ivan不可能用A过 牌。他不应该用Q跟注，被过牌的话也不应该用它下注。

平衡情况下，Ivan绝不会选择在转牌圈过牌然后在河牌圈下注，因为在转牌圈过牌之后他没有可以用来平衡诈唬的价值下注。他在转牌圈过牌之后丢掉底池看起来是一个耻辱，但是不管他诈不诈唬， 他拿着Q时的期望值都是$0。如果他拿着A，就不值得牺牲转牌圈下 注的价值去建立转牌圈过牌和河牌圈诈唬的两极化范围。

跟单回合游戏一样，Ivan的欺骗并不是在拿着坚果牌时做手脚，而是用诈唬来平衡价值下注。两回合游戏的复杂性在于他必须先找出 盈利最高的方式去玩价值牌型，然后找到合适的诈唬策略去平衡。

4.Ivan拿着Q的时候在转牌圈的下注频率会比河牌圈的高还是低还是 一样呢？

更高。在原始透视游戏中我们看到如果Ivan下注$1到大小为$2的底池，那么3:1的价值下注诈唬比会使得抓诈唬牌对于弃牌和跟注单个 下注不偏不倚。不过，在这个游戏中，抓诈唬玩家有三个选择：在转牌圈弃牌，在转牌圈跟注且计划在河牌圈弃牌，或者在转牌圈跟注且计划在河牌圈跟注。Ivan的策略必须使得Opal对于这三个选择都不偏不倚。在转牌圈弃牌的期望值是$0，所以他必须采用这样一个诈唬策略，使得Opal其他选择的期望值也是$0。

我们从在转牌圈跟注然后在河牌圈弃牌说起。从原始透视游戏中我们知道，如果Opal在转牌圈跟注，Ivan的河牌圈策略就是用所有As 和1/3的Qs（所有Qs的1/3而不是在转牌圈下注的Qs的1/3）或者4/6的 起始范围往大小为$4的底池投入最后的$2。

如果Opal在转牌圈跟注并计划在河牌圈弃牌，她的EV = $3 * (%在 河牌圈过牌) – $1 * (%在河牌圈下注)。换言之，如果Ivan在转牌圈诈唬，在河牌圈过牌，那么Opal能赢$3。如果Ivan在河牌圈再次下注（不管是价值下注还是诈唬），Opal弃牌并输掉$1的转牌圈下注。

如果我们把4/6代入%在河牌圈下注并解%在河牌圈过牌，可得 4/18。这意味着Ivan应该用4/18的范围在转牌圈下注，在河牌圈过牌。当然，他决不应该用A在河牌圈过牌，所以他的过牌范围只包括Qs。Qs只占他范围的一半，所以为了达到在河牌圈用4/18的范围 过牌的频率，他应该用8/18的Qs在转牌圈下注，在河牌圈过牌。这 是除去在转牌圈下注然后在河牌圈再次下注的1/3或6/18的Qs之外的，所以他一共会用14/18的Qs在转牌圈下注！

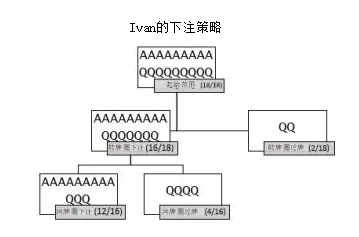
功能上来说，她在转牌圈的价值范围是所有的As加上所有会再次在 河牌圈下注的Qs。他会用整个“价值范围”的1/3去诈唬，用以平衡，然后在河牌圈过牌。

如果还有第三个下注回合，有效筹码量还够另一个半底池下注， Ivan可以把在转牌圈下注的范围的16/18当作第一个下注回合的“价值范围”，再用16/54的范围去诈唬，以平衡这个价值范围。那就是 所有的Qs，然后是其中的一些，这就意味着他会用整个范围下注。尽管Opal可以马上得到3:1的底池赔率，而且知道她有一半的几率拿 到最佳牌型，但她的最佳策略还是在翻牌圈100%弃牌。Ivan会在后面回合施加太多压力。这就是杠杆作用的威力。

5.Opal在转牌圈的跟注频率会比河牌圈跟注频率高还是低还是一样呢？

一样。跟往常一样，Opal拿着K时能采取的最佳策略是找到这样一 个跟注频率，使得对手对于下注和用Q过牌不偏不倚。

首先，我们要知道Ivan在转牌圈用Q过牌的期望值是$0。这可能不明显，因为还有一个下注回合，所以假设Ivan要在转牌圈过牌，然后在河牌圈下注。Opal的策略是关注下注的底池赔率，然后找到这 样一个跟注频率，使得诈唬期望值为$0。如果Ivan拿着Q时在转牌圈和河牌圈过牌到底，那么价值就是$0。不管他在转牌圈过牌之后 会采取什么行动，他拿着Q时的期望值都是$0。

因为Ivan在转牌圈用Q过牌的期望值是$0，所以Opal必须找到这样一 个跟注策略，使得用Q下注的期望值也是$0。Ivan的期望值等于$2* %弃牌 + %跟注 * (EV被跟注 – $1).最后一个项(EV被跟注 –   $1)比较棘手。Ivan不会只是因为Opal跟注了他的转牌圈诈唬就自动丢掉底池。他还是可以进入河牌圈，也有 可能赢下底池。他往底池投入了$1，所以最后不管他拿到的钱是多 少，都要扣掉这$1。

Ivan拿着Q时在河牌圈的期望值是多少？这个结果跟透视游戏是一 样的，都是$0。Opal在转牌圈跟注之后，Ivan可以在河牌圈过牌（期望值是$0）或者再次诈唬。如果他再次诈唬，Opal会用一个使 得他的期望值为$0的频率跟注。不管怎么做，Ivan在河牌圈拿着Q 的期望值都是$0。

所以，这个方程可以简化为EV = $2 * (1 – %跟注) – $1 * %跟注。如果我们令EV为$0，解%跟注，我们可以得到2/3，这跟单回合游戏中 对抗半底池大小下注时的抓诈唬频率是一样的。

如果Ivan采取不同的下注尺度（偏离平衡策略），那么这个数字就不会这么明确，因为Opal要根据下注尺度调整跟注频率。原理是一 样的：每次面对下注，Opal都会设想当前范围——鉴于她目前采取 过的行动，她现在可能拿到的牌型——然后用足够的牌型跟注，使得Ivan在这个决策点对于诈唬不偏不倚。

对于拿着被压缩范围的玩家来说，数学运算过程会简单一点，但是她所处的情况要糟糕得多。尽管前注是$1，但她在这个游戏中的期望值只有$0.22。在有效筹码量为$3的单回合下注游戏中，她的期望 值是$0.40，这说明对于拿着两极化范围的玩家来说，把下注分散到 各个回合是多么有利，即使他的总下注金额是一样的。

6.假设下了前注之后有效筹码量是$24。Ivan在转牌圈的下注尺度应 该是多少？下注范围是什么？

Ivan应该用整个范围在转牌圈下注$4。这是一个两倍于底池大小的下注，这样就建立了一个两倍于底池大小的河牌圈全压下注。回想 一下，拿着两极化范围的玩家的最佳下注尺度是底池的几何增长， 意味着在两个回合中Ivan应该用底池大小的相同比例下注，使得最后的下注是全压。

他的河牌圈范围应该包括所有的As和2/3的Qs，即每三次价值下注就有两次诈唬。这个比例来自下注/(下注 + 底池)方程，这个情形中的结果是$4/$6。

在转牌圈，Ivan用所有他会在河牌圈下注的牌型加上足够的诈唬牌型下注，这两种牌型的比例是2:3。不过在这个情形中，他达到这个 比例之前Qs就不够用了，所以他的最佳策略是在转牌圈用所有Qs下 注，然后在河牌圈弃掉其中的1/3，用另外2/3再次诈唬。

不过应该不至于到这个地步，因为Opal的最佳策略是100%弃牌。两 极化范围加上高筹码底池比使得Ivan有很强的杠杆作用，所以Opal 的最佳策略就是在第一个机会弃牌！

当前面位置的加注者跟大盲位置跟注者在翻牌圈单挑，你就会看到 这个动态。在正确的翻牌圈牌面中，由于杠杆作用，加注者可以通 过用任意两张牌诈唬盈利。在下一章中，我们会探索这个场景。

当然，对手可能不知道你拿着同花听牌。他可能会错误地在空白转 牌过牌，让你可以在河牌圈实现剩余的胜率。当你成了同花之后， 他还有可能错误地下注或者跟注。当你错过了同花，他还有可能错 误地弃牌！尽管我们不能给到这些因素一个准确的数字，但是它们 都会影响到跟注翻牌圈下注的期望值。

胜率实现是用来概念化后面回合的下注会如何影响某手牌的方法。可以把它看成系数r，这是连接胜率和期望值的桥梁。用胜率乘以胜 率实现就可以得到一手牌的期望值；胜率 * r = 期望值。

思考Opal在两回合透视游戏中面对$1的转牌圈下注。对抗Ivan的平衡下注范围时，她的K胜率大概是44%。如果她可以跟注并直接摊 牌，期望值是$3的底池中的$1.32，她不会对跟注和弃牌不偏不倚；跟注对她来说非常有利可图。不过，跟注的平衡期望值是$0，因为她在河牌圈对抗平衡的两极化范围时没有办法捍卫胜率。

那损失的底池份额哪儿去了呢？这是个零和游戏，所以这部分肯定 到了Ivan和他的两极化范围手里。他的两极化范围中的哪手牌由于杠杆作用而增加了期望值就很难概念化了。

对抗Opal的平衡跟注策略时，我们知道Q的期望值是$0，所以她损失的期望值会落到Ivan的As。事实上，Opal跟注翻牌圈下注之后，  A的平衡期望值是$5.33，但它的胜率只有$4，即底池大小。额外的$1.33来自Opal有2/3的几率在河牌圈损失$2的下注。因此，Ivan的As的r是$5.33/$4 = 1.33。r大于1代表它们会从后面回合下注中获利。

不过Opal不需要用2/3的频率跟注河牌圈下注。她的跟注频率可以更 高，这样Ivan的As的期望值会更高，而Qs的期望值是负的。她也可以100%弃牌，这样Ivan的As的期望值是$4，Qs的期望值是$1.33， 因为它们诈唬的话有1/3的几率能赢到$4的底池。不管Opal选择什么 策略，她都会对平衡下注范围放弃$1.33的期望值。通过弃牌更多或 更少，她能决定Ivan范围内的哪手牌可以得到期望值，但是她没有办法减少自己的损失。

可以在未来的决策点通过下注（不管是价值还是诈唬）盈利的牌型 有实现高于胜率的价值的潜力，而纯抓诈唬牌能实现的价值一般比 自身胜率小。这个例子中，我们看到价值牌的期望值高于自身胜 率，而诈唬牌则不是，至少平衡情况下不是。之后我们会看到后面 回合中有利可图的诈唬的可能性会如何提高弱牌的期望值。

弱牌有潜力去实现超过胜率的期望值，这一点不能使它们优于抓诈唬牌。Opal的K实现的价值低于胜率，但是它还是比Ivan的Q要好， 期望值也更高。如果你的胜率是0，超额实现胜率是很容易的。胜率实现并不是衡量牌型的绝对价值的手段；它只是比单独用胜率去衡量一手牌的价值更好。

胜率实现跟环境息息相关。它取决于位置，牌面结构，筹码量和玩 家的范围组成等因素。我们不能在真空环境中得出“A9o的胜率实现很糟糕”这样的结论，也不能说“A9o是一手糟糕的牌”。

如果两位玩家在后面回合都采取平衡策略，解算器可以得出确切的 期望值，但实战中这种情况很少发生。你需要估计一手牌未来的期 望值或胜率实现。在牌桌下做好准确的计算可以帮助你在赛场上作 出更好的估算。

场景：两回合透视游戏中的剥削

制定剥削策略可以很好地测试你对平衡的理解程度。如果你明白为 什么平衡策略是这样的，那么你就有能力去思考和剥削偏离平衡的 策略。如果你觉得这些问题无从下手，那你可以回顾一下两回合透 视游戏的平衡策略的解释。

每个玩家的前注是$1，还剩下$3的后手筹码。Opal总会拿到K，而Ivan随机拿到A或Q。玩家都知道彼此的范围。

有两个下注回合，但是牌型价值不会改变。Opal总是过牌。Ivan可 能会过牌或者下注，下注尺度在$1- $3之间。

3.假设Opal会100%对$2或更大的河牌圈下注弃牌，但我们不知道她的转牌圈跟注策略。Ivan的利益最大化剥削策略是什么呢？

4.假设Opal在转牌圈跟注的话会100%在河牌圈跟注，但是Ivan不知 道她的转牌圈跟注策略。他的利益最大化剥削型策略是什么呢？

5.假设在转牌圈下注$1之后，Ivan会在河牌圈100%用As下注$1，用Qs下注$2。Opal的利益最大化剥削型策略是什么呢？

如果Opal跟注这个下注，然后在河牌圈遇上另一个下注，那这个下注应该是$1进入$4的底池，所以她的跟注频率应该是4/5。

Ivan选择这个下注尺度的的期望值只有$1.52，而他平衡策略的期望值$1.78。Opal没有主动剥削他的错误，他就已经损失了这个价 值。她只是用使得他对于所有他选择的下注尺度的诈唬都不偏不倚 的频率去跟注。如果他选择了次最优尺度，那么他获得的价值就比 平衡策略少。

2.假设Ivan在转牌圈下注$1，Opal知道他的范围包括所有的As和1/3的Qs。她的跟注频率应该为多少？

Opal应该在转牌圈100%弃牌！

设想平衡策略：Ivan应该用7/9的Qs下注，使得Opal对于在转牌圈弃牌，在转牌圈跟注然后在河牌圈弃牌，以及在转牌圈跟注然后在河牌圈跟注之间不偏不倚。

读牌：Ivan不会在转牌圈进行足够的诈唬。

确定剥削策略：我们知道Ivan可以通过在河牌圈用所有As和1/3的Qs 下注而盈利，在不知道他的策略的情况下，我们应该假设他会这么做。所以Opal不应该在转牌圈跟注然后在河牌圈弃牌，因为Ivan的整个转牌圈下注范围也会用于在河牌圈下注。她应该假设她看到摊牌的赔率是$3投入$8的底池，意味着她胜出的频率要大于3/8才能盈 利。她最多只有1/4的几率胜出（Ivan拿着Q），所以她最好是马上弃牌。

确定偏离程度：Ivan的偏离程度很小，但是因为Opal在平衡情况下对于所有选择不偏不倚，所以即使很小的偏离都会对她的策略产生 很大的影响。她没有在转牌圈跟注的动机，因为她不能指望在不投 入$3的情况下就赢下底池。

即使我们读出来Ivan在河牌圈的诈唬频率会不够，那也不值得Opal 在转牌圈跟注。最好的场景是，如果她知道Ivan绝不会在河牌圈诈唬，那么她就可以在对抗他的Qs时赢下底池，在他拿着As时弃牌， 从而避免输掉第二次下注。这样她的期望值是$0，所以她最多能让转牌圈下注不赔不赚。但凡Ivan在河牌圈有一丁点诈唬，她就会输钱。

很多玩家都会表现得好像在转牌圈诈唬之后就必须要在河牌圈再次 诈唬一样。事实上，你的转牌圈下注范围要包括一些会在河牌圈弃 牌的诈唬牌，不然对手没有动机在转牌圈跟注然后在河牌圈弃牌。如果对手知道你在转牌圈诈唬之后一定会在河牌圈诈唬，那他就不 会用不想用来摊牌的牌型在转牌圈跟注，这样就能剥削你。

3.假设会100%对$2会更大的河牌圈下注弃牌，但我们不知道她的转 牌圈跟注策略。Ivan的利益最大化剥削策略是什么？

Ivan应该用全部范围在转牌圈下注$1，被跟注的话在河牌圈全压。

设想平衡策略：Opal应该在转牌圈用2/3的牌型跟注，然后在河牌圈用2/3的牌型跟注。这使得Ivan对于在转牌圈过牌，在转牌圈诈唬然后在河牌圈过牌，在转牌圈诈唬然后在河牌圈诈唬不偏不倚。

读牌：Opal在河牌圈的弃牌频率太高。

确定剥削策略：Ivan希望利用这个$2的河牌圈下注尽可能诈唬。这意味着他需要把尽可能多的诈唬牌带进河牌圈。他有两种方式进入 河牌圈：在转牌圈过牌，或者下注$1，剩下$2。他倾向于选择后 者，因为如果Opal跟注$1然后在河牌圈弃牌，对于Ivan来说这比他过牌然后用河牌圈诈唬赢下$2的底池要好。

技术上来说，因为我们只规定了Opal要对$2的河牌圈下注弃牌， Ivan可以在拿着As时稍微减小下注尺度，但是Opal没有理由投钱给他。如果要在河牌圈弃牌，那Opal的最佳策略就是直接在转牌圈弃 牌。这样她就只会输掉前注，鉴于她的河牌圈错误，这是她的最优 解了。如果Ivan剥削她的河牌圈弃牌，那么所有包含转牌圈跟注的策略都会导致她的损失大于前注。

确定偏离程度：很大。如果可以的话，Ivan还会进行更多诈唬。不幸的是，如果他用所有Qs下注，他的诈唬牌型就不够了。

4.假设Opal在转牌圈跟注的话会100%在河牌圈跟注，但是Ivan不知

道她的转牌圈跟注策略。他的利益最大化剥削型策略是什么呢？

Ivan应该在转牌圈用全部范围下注$1，然后在河牌圈用As全压，弃 掉Qs。

设想平衡策略：Opal应该在转牌圈用2/3的范围跟注，然后在河牌圈用2/3的牌型跟注。这使得Ivan对于在转牌圈过牌，在转牌圈诈唬然后在河牌圈过牌，以及在转牌圈诈唬然后在河牌圈诈唬不偏不倚。

读牌：Opal在河牌圈的跟注频率太高。

确定剥削策略：Opal在河牌圈的跟注频率太高，那么试图不在河牌圈诈唬就是明显的剥削。不过，如果在转牌圈跟注意味着要在河牌 圈跟注，那Opal的最佳策略就是在转牌圈弃牌。这给了Ivan在转牌圈诈唬的动机，即使他不会在河牌圈坚持到底。

确定偏离程度：很大。如果Ivan相信Opal不会弃牌，那他就不应该 在河牌圈诈唬。但是，因为Opal有额外的动机在转牌圈弃牌，所以Ivan可以提高他的转牌圈诈唬频率。他的利益最大化剥削策略是用全部范围下注，在河牌圈的价值下注诈唬比为1:1，然后在河牌圈放 弃掉所有诈唬。这使得Opal对于跟注两次和直接在转牌圈弃牌不偏不倚。她的最优应对策略是在转牌圈跟注，在河牌圈弃牌，但是我们规定了她不能这么做。Ivan剥削的是她在转牌圈跟注然后在河牌圈弃牌的错误 。

5.假设在转牌圈下注$1之后，Ivan会在河牌圈100%用As下注$1，用Qs下注$2。Opal的利益最大化剥削型策略是什么呢？

Opal应该100%在转牌圈跟注，然后对$1的河牌圈下注弃牌，跟注$2的河牌圈下注。

设想平衡策略：Ivan应该在河牌圈进行尺度大小相同的价值下注和诈唬，这样他的对手就无法预测他是在价值下注还是诈唬。

读牌：Ivan通过河牌圈下注尺度表现牌型牌力。

确定剥削策略：Opal应该100%对$1的河牌圈下注弃牌，跟注$2的下注。鉴于她可能会由于Ivan的河牌圈错误获利，所以她不会对跟注转牌圈的下注不偏不倚；她应该100%跟注，从而最大化在河牌圈剥 削他的机会。

确定偏离程度：很大。扑克游戏里面发牌的时候牌面朝下是有原因的：清楚地暴露的你的牌型的策略都要负主要责任！

在玩具游戏的背景下，Ivan的策略听起来很荒唐，但很多真实扑克玩家都会这么玩。或者他们会选择相反的策略，用强牌下更大的 注。这么做有一个好的剥削理由——如果Opal对$2的下注弃牌频率 太高，对$1的下注跟注频率太高，那么Ivan的这个策略就是利益最大化剥削策略——但不是标准策略。

这听起来很符合逻辑：玩家拿着强牌时，他们想要被跟注，所以他 们下小注。拿着弱牌时，他们想要对手弃牌，所以他们下大注。

这里例子阐明了这个方法的缺点。你应该警惕会暴露你的牌型牌力 的下注尺度策略，尤其是对抗娴熟的对手时。这样的玩家非常善于 捕捉你泄漏的任何信息。

比较A♠Q♠在Q♦7♣2♥翻牌和在Q♦9♦7♣翻牌中的情况。在两个牌面 中，你都有顶对带最强踢脚，但是把2♥换成9♦就极大改变了你的牌 型在后面回合的价值。

在前一个牌面中，你的牌型可能强到可以用来在转牌圈价值下注， 甚至可能在河牌圈也能价值下注。在后一个牌面中，大部分的转牌 都会带来新的威胁。可能是潜在的顺子，潜在的同花，或者甚至把 你的对子降为第二大对子的K。

如果有效筹码量足够浅，使你可以在翻牌圈全压或者下注大部分筹 码，那这个差别就没那么重要。不过，如果筹码量很深，那你从前 一个翻牌下注中得到的盈利比从后一个下注中得到的要多得多。

如果在第一个翻牌圈的下注被跟注了，你不仅能从即时胜率优势中 盈利，还能从增长的底池中获利，这样你能在转牌圈下更大的注。如果你想在第二个牌面增大底池，很多转牌都会让你后悔这个决 定。

并不是说下注就一定是错的。在第二个牌面中AQ依然是最强的牌 型，而且在这个情形中，下注可能比过牌好。但是，AQ从未来的下 注中能得到的预期收益会更少，而且你不能像本章描述过的一样继续把下注作为两极化范围策略的一部分。

在考虑一个牌面稳不稳定时，很多玩家会把重点放在是否存在顺子 听牌和同花听牌上。不过，通常来说，决定一个牌面稳不稳定的最 大的因素是牌的大小。在AK2翻牌中，翻牌圈的顶对或第二大对子 在河牌圈依然是顶对或第二大对子，翻牌圈中的非对子在大部分河 牌圈都依然是弱牌，即使成了对子。在872牌面中，在翻牌圈击中的对子就要脆弱得多，几乎所有非对子都有潜力提升为顶对。

对子和同花的存在也会使牌面更为稳定。在同花色或者成对子的翻牌中，最强的牌型在河牌圈可能依然是最强的。

你的对手错过了很多次加注的机会，所以他在转牌圈的范围是被压 缩的。2♥不能改变这个局面。

不过，你的范围里有很多坚果牌。根据牌面不同，像KQ这么弱的牌 型也有可能强到可以用于争取筹码。如果你确实拿着强牌，你不能指望对手去下注和加注，因为拿着被压缩范围的玩家是不应该这么玩的。从你的强牌中获得价值的方法是下大注，让诈唬的威胁给你的对手提供跟注的动机。

大尺度下注给你的对手提供了糟糕的跟注赔率，这样你可以往下注范围内加入很多诈唬牌。因为你可以期望在很多河牌圈中继续用两极化范围下注，所以这个杠杆效应可以支撑你在转牌圈进行更多诈唬。

坚果牌优势加上深有效筹码量让你可以用两极化范围进行包含很多诈唬的大尺度杠杆下注，而这就是一个很好的诈唬候选。如果你可以在转牌圈用底池的75%或150%下注，那么这里的平衡策略就 是用45%的范围超池下注！

2.你下注$100，对手跟注，河牌是3♠。对手过牌。有效筹码量为$365，底池大小为$270。你的策略是什么？过牌。很多玩家会犹豫什么时候放弃诈唬。从范围构建的角度去思考会大 有帮助。

“如果我过牌了就没法赢，但是这是很好的惊悚牌，我似乎可以假装拿到了同花，就试一下吧。”，这样的想法是很诱人的。  不过， 如果按照这个逻辑，你根本就不会放弃任何诈唬。毕竟你的下注理由跟你的手牌无关，所以在你拿着弱牌时也适用。

两回合透视游戏展示了100%的诈唬会如何被剥削。如果你读牌发现 对手在这个情形中会过度弃牌，那么出于剥削性的原因，用所有的弱牌再次下注可能是正确的。不过，平衡策略是用一些牌型诈唬， 并弃掉一些牌型。

在我们的玩具游戏中，Ivan只有一个诈唬候选，所以他唯一要做的决策是决定在每个回合以什么样的频率用这手牌下注。在实战中， 你可以，也应该根据手上的牌去做这个决策，因为有一些牌比其他 牌更适合诈唬。

在这个情形中，最佳诈唬牌型包括黑桃，这样你的对手拿着同花的 可能性就变小了。理想情况下，你通过在转牌圈用A♠Q♥这样的牌型诈唬，提前为黑桃河牌做好准备。

你的8♦7♦用于诈唬的话就没那么有吸引力，因为它不能阻断同花。

如果你有疑问，不要考虑河牌（或转牌）是否适合诈唬，而是要确 定你的诈唬范围和过牌范围是不是都有弱牌。然后决定哪个范围更 适合加入你手上的牌型。

3.你在玩锦标赛，小盲是1K，大盲是2K，前注是2K。在满员桌中， 你拿着A♠K♠第一个行动，加注到4500，大盲位置玩家跟注。翻牌 发出T♥8♠6♥，大盲位置玩家过牌。底池有12K，你和大盲位置玩家  都还剩下100K。你的策略是什么？

过牌。

这个翻牌对前面位置的加注者不是很友好，所以他不能随意对大盲 位置跟注者进行下注。尽管你相对大盲位置玩家依然有胜率优势， 但你没有坚果牌优势。大盲位置玩家范围内的弱牌比你多，但是他也会有更多同花，两对和三条这样的组合。

这是坚果牌优势，不是胜率优势，它使得玩家可以利用杠杆作用， 在翻牌圈用不成比例的诈唬逃脱。在这个情形中，如果你下注，你就要担心遇上自带杠杆作用的过牌-加注，这样你就很难实现胜率和 用边缘牌型摊牌。

过牌-加注的威胁使得用A♠K♠这样胜率不错但是不足以跟注对方的加注的牌型来下注变得没有吸引力。下注然后对T♦7♦的加注进行弃 牌就够糟糕了，但是下注然后对K♥7♥的过牌-加注进行弃牌就是灾难了。

如果没有杠杆作用的加持，你无法在翻牌圈用尽可能多的诈唬逃 脱。鉴于过牌-加注的风险，你应该用更为两极化的范围下注，包括 很强但是易受攻击的牌型，例如JJ，强到足以跟注对手的加注的听牌，例如Q♥J♥，以及面对过牌-加注时可以弃牌的牌型，例如 A♦2♦。

拿着A♠K♠的时候，你会希望底池尽可能小，尽量向摊牌靠近，并且可以看到下一张牌，这样你有比较大的概率可以得到顶对或者听 牌。

你冒着让自己陷入思维困境的危险，试着去猜你的对手会不会在后 面回合继续下注，如果你猜错了，就要付出昂贵的代价。Opal不用 担心这一点。如果Ivan下注，Opal会找到这样一个跟注策略，使得他对于诈唬当前下注不偏不倚。如果他再次下注，她自有办法。

这个玩具游戏描述了拿着被限制（capped）的范围时有多糟糕，它使得你的对手可以用宽的两极化范围攻击你。在真实无限注德州扑克中，很少会出现跟两回合透视游戏一模一样的情形，但是很大一部分原因是因为避免这样的情形是核心战略方针。在研究实际的德州扑克情形时，我们会看到大部分策略都围绕着如何使你的范围不被限制，如何呈现两极化范围的威胁，以及阻止对手用杠杆作用实现优势。

♠   跟注并使得对手对于诈唬当前的下注不偏不倚。用被压缩的范围去对抗两极化范围的杠杆下注并不有利可图，但也没那么难。当你的对手下注，你用熟悉的公式去找到不可剥削跟注频率。如果 他再次下注，那么你可以把这个公式代入当前范围并跟注。

♠ 最好的防御是回避。尤其是还剩下很多钱的时候，要避免你的范围被限制，以防你被对手用两极化范围下大注。

♠  在实战中，牌型价值很少是稳定的。如果不是这样，那你就要衡量用两极化范围下注的好处  vs    否定胜率和对手的未来机会的价值。

♠  前面回合的诈唬牌通常有机会提升到可以获胜的牌型。这就使得我们计算使得对手不偏不倚的运算更为复杂，而且可能会给拿着被 压缩范围的玩家用中等牌力牌型下注或者加注的动机。