第三节:殿堂级全压算法
有时候会有人过来问我在看什么,我告诉他们“这是我的扑克系统。”甚至我会向他们展示图表,然后他们也不知道我实际在做什么。
我看过2019 WOP主赛回放并且不断问自己:“在那种情况下我会怎么做?我真的能在国家电视台直播现场看自己的小抄吗?”虽然这可能不算违规,但我更希望自己的对手不知道我是如何做出GTO决定的。所以我开始思考能如何简化LUSE系统以便我能记忆。这在后来就成为了我的GTO殿堂级打法。
模式叠加
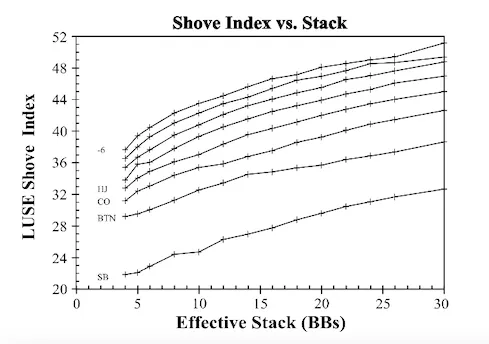
(图4.3a。每一个桌位LUSE全压指数VS有效筹码量的坐标图)
让我们来看看这些曲线的斜率,它们似乎在6到20BB有效筹码量之间普遍呈线性。这也是全压最为重要的区域。图4.3b“数据”栏中总结出了斜率和截距的最佳匹配值。
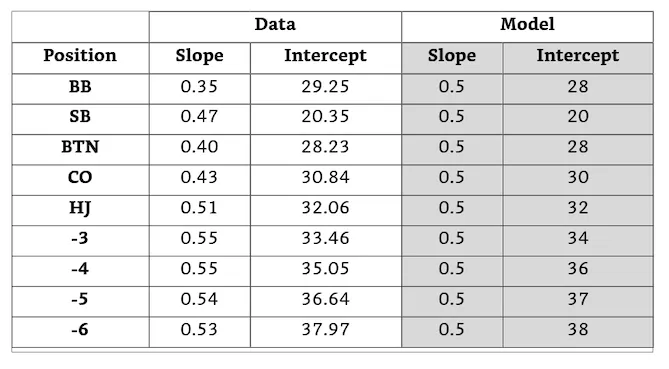
(图4.3b,“数据”栏中为图4.3a中6-20BB曲线的斜率和截距。“模型”栏中为斜率为0.5时的模型结果。)
我们看见这些斜率和截距都在0.35和0.55之间变化,实际上都是非常相似的。如果我们能够记住这些斜率和截距,并且如果我们能在脑海里进行计算,我们就可以在不看任何笔记的情况下在线下锦标赛中使用这些精确的GTO全压范围。
虽然我们中的一些人或许能够使用这种方法,但对于其他人来说一个更简单的方法可能更为实用。一种简化的方法是针对每种筹码尺度使用统一的斜率,另一种方法是针对截距使用整数值。
这些斜率的平均值是0.48,所以0.50的斜率对我们的模型而言是一个中间选择,有利于我们在牌桌上非常容易的使用。如今我们有了针对GTO全压的殿堂级算法:
全压指数=(位置指数)+筹码/2
这算法的使用非常简单。我们只需要:
n 筹码量(以BB为单位)除以2或乘以0.5。
n 加上一个取决于我们的牌桌位置指数(PI)的整数值。

(图4.3c。殿堂级位置指数。)
这在线下牌桌非常容易实现。其实,你可以将牌桌位置指数刻在你的压牌器上。牌桌位置指数(PI)是殿堂级系统的关键所在。它会被用于我们全部的GTO决定,包括跟注和再全压。
最后强调一点,从大盲位开池全压是没有位置指数的。如果小盲位进行开池,那么我们可以用PI=28,如图4.2b建议的那样。但这也是存在问题的,因为我们根本不知道小盲位的全部范围。正因为我们能够查看自己的选项,所以我们基本上应该做一个正确的扑克决定。在图4.3c中大盲位的PI为18被用于跟注一个全压和在大盲位的再全压行动。
殿堂级算法误差
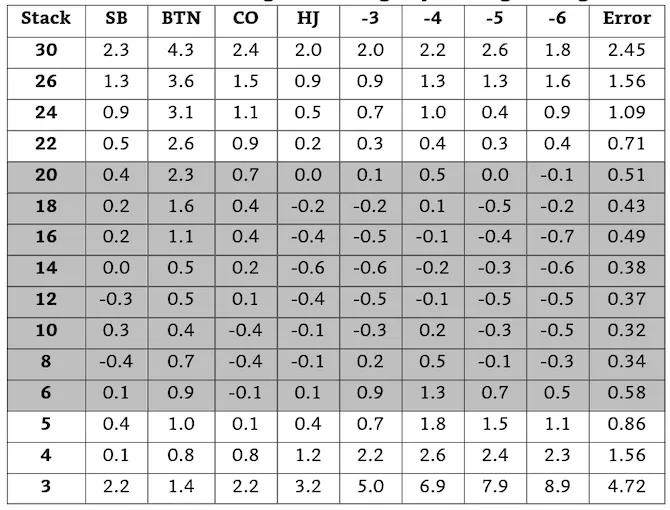
(图4.3d,殿堂级全压中所产生的LUSE指数误差。阴影区域代表优化区域。“误差”是该行的平均绝对误差。)
我们能看见殿堂级模型通常是相当准确的,即使存在误差。平均绝对误差在6-20BB区域内为0.43。对于筹码量不高于5BB和不低于24BB的情况来说误差仍然是非常小的。
因此,我们认为殿堂级全压指数的使用极限应该设置在5-24BB。我们应该认识到随着偏离这个区域,我们的全压指数会逐渐趋于保守。
幸运的是,这并不是什么限制,因为我们通常不太会全推一个30BB筹码量,而且我们的筹码量通常也不会有4BB。由于我们不会全压+EV非常低的底线手牌,所以变得保守一点也没什么损失。
这组特殊的位置指数并不是我们唯一可以选择的。其实,一些存在些许误差的其他选择与之有关。但这个选择的好处就在于在线下赛事中容易记忆。而且它与我们后来章节将介绍的其他指数有着很好的配合。
当我们利用近似值并接受小的误差时,我们可以争论这是否是一个真正的GTO系统。或许我们能够称之为准GTO,尽管我们在整本书中都叫它GTO。
注意,即使是小误差,它所产生的结果也远远好于我们试图记忆图表所行动的结果。
第四节:精准度
GTO解算器精准度
这个问题在真正的锦标赛中并不重要,毕竟无论如何人类玩家都无法做出完美的GTO决定。况且几乎没有人来选手能够识别出对手的GTO小错误,更别说根据错误进行剥削性打法调整。
因此,人类玩家不一定要做出完美GTO决定去割手GTO策略红利。比如,如果你当下的牌况表明恰当的GTO全压范围是50%,那么用一个48%或52%范围全压不会有什么损失。一个适当范围的知识点变得不那么重要。
所以,在剥削性和盈利性没有变化的情况下,我们可以用一个边缘性弃牌组合代替一个边缘线全压组合。
CPI模型精准度
这说明由组合牌力指数建立的手牌排序并不完美。

(图4.4,针对每一组起手牌的全压EV与积累范围图。庄位筹码量16BB)
但当我们使用LUSE系统的时候,这种不完美并没有明显降低我们的EV。假设我们用一个LUSE为35的指数全压,也就是35.4%的范围(虚线)。符号“O”代表一个组合的全压误差。比如,我们可以用Q9o和Q8o全压,尽管这些组合毫无收益。另外七个组合都为弃牌误差(+符号);不全压它们的损失会小一点。
这些错误的平均误差约为0.13BB。但我们这里全压的69手牌中有63手的EV都远高于这个数值。所以此类误差的净效益并不会明显影响我们的整体预期,甚至是在对抗一名完美对手的时候。
将此与开池弃牌AA的失误进行对比。以EV为5.95BB进行计算,这将是46倍的高昂代价。或者这么认为,这个平均失误还不及我们16BB全压的百分之一。
这对于我们LUSE系统内置的小误差存在着重要影响。不产生这类边缘性误差的LUSE系统是不可能被创建出来的。但它们可以与我们GTO模型中的其他误差进行对比,比如我们对有效筹码尺度的不准确估计。我们能在线下锦标赛中使用的任何简化系统都会一直存在这些误差。
幸运的是,我们永远不会在线下锦标赛中碰到一名完美的对手,甚至是实力接近完美的人。我们或许会遇到一名厉害的GTO线上玩家,TA有无数可利用的图表或能够利用GTO程序。但即使是这样,他们的表现也不会很完美。
在对抗典型对手和他们所犯的错误时,我们应该保持最好的状态。因为我们一直可以选择调整自己的范围来剥削他们,我们的LUSE全压范围能够被视为只是一个底线。
因此,我们不需要过度担心简化后的殿堂级策略所存在的小失误。如果我们偏离LUSE一到两个点,这其实并不怎么重要。






评论 ( 0 )