控制你的短期形象
我们可以通过在一个特定的牌况中变得或多或少的激进来控制我们的形象,或者是用边缘牌进入摊牌环节,当我们可以通过诈唬收池时就可以慢打自己的底牌。但是,一定要警惕那些轻易释放出来的信息,很可能是个圈套。对手也有可能搞明白我们慢打的原因,然后根据情况调整打法。
同时,当你诈唬后摊开底牌时,你不仅仅是在向对手展示自己的诈唬,对手也明确地知道了你接下来的打法。
所以即使展示诈唬是让对手相信你的牌风,你其实也是在一个短期的优势中为自己树立了一个长期的形象。
你在某个牌况中的形象是有可能影响在另一个牌况中的形象的。比如,如果翻前你突然3bet某人,那么对手可能会直接认为你在翻后也是激进的,并且也会开始调整对你的认识。如果面对3bet你已经多次弃牌于某人,这名对手就会认定你是可以在翻牌圈被全压的并加注你的全部持续性下注。
换言之,在连续的多手牌中你已经3bet了某人很多次,此时在一个翻后底池中碰到他,他就会觉得你翻后策略同样也是激进的。此时你的应对策略就是通过用强牌采取激进打法来剥削对手(不是慢打),拿到弱牌时采取更为被动的打法。
最关键的是要不断地意识到牌桌上每位玩家如何看待你的形象,并思考如何改变这种形象,使对手在对抗你时发挥更差。当然,有些玩家会比其他人更能适应你给他们的信息。同时游戏16桌的人比同时游戏4桌的人更不可能注意到你对他们进行了连续5次的3bet。此外,有些玩家,包括一些只玩四桌的玩家,采取的是一种非常可靠稳定的策略,根本不会对你进行调整。所以试着找出你可以操纵的玩家并创造性地对抗他们。
解读和手牌历史
比如,如果我们注意到对手跟注河牌圈过于松散,我们就能通过线性价值下注来剥削他的这个错误。但如果对手转换成正确的策略,我们也仍然可以剥削他的老错误,只是我们会输钱。所以为了剥削一个弱点,我们需要保证存在和持续存在的问题。
用更为博弈论的话来说就是:通常我们会尝试用一种最佳的非剥削式的打法游戏。这意味着如果对手犯错且打法不是最佳,通过偏离纳什均衡策略他会直接输钱。此时我们要么调整自己的策略(剥削对手的错误)要么保持打法不变。如果我们保持打法不变,我们就一定能从对手的错误中获益。
但如果我们从纳什均衡策略转化成一个剥削策略,我们就能从对手的缺陷策略中获得更多利益。然而,如果某个时候对手再次实施纳什均衡策略,并且我们没有及时调整过来,我们的策略就会变成非最佳策略从而致使输钱。最差的情况无非是对手开始游戏一个剥削策略,我们迅速输钱。
调整我们的解读策略
从对手的行动来看,我们感觉他似乎总有一张弱黑桃牌。对手知道我们拿到一张强黑桃牌的概率为20%,没牌的概率为80%。我们发现于我们而言最佳策略就是在没有同花成牌的情况下(10.7%)全压,那么此时对手的期望值就是$571.43。但是,这个概率的准确性是基于对手也采取最佳打法的假设中。
如果我们在早起的手牌中观察到对手不愿意放弃看似强劲的底牌,即使很明显他可能会被击败,那么我们可以保守地认为在对抗我们的全压时他不会弃掉自己的弱同花。于我们来说不幸的是,通过游戏纳什均衡策略,我们无法从这个缺陷中获利。这是因为我们的策略是被设计的以至于对手的跟注期望值等于弃牌的期望值。但在这个牌况中,如果我们偏离纳什均衡,我们就算是进步。
所以如果对手一直跟注,我们就绝不该诈唬,而且在我们拿到强同花牌时就该一直价值下注。这说明对手赢得$800底池的概率为80%,输掉$2000底池的概率为20%(代价就是牺牲掉一个$600的下注),此时对手的期望值就是$520。
(0.8)($800)+(0.2)(-$600)=$520
因此,通过改变自己的策略去剥削对手,我们获得的期望值为$51.43。
$571.43-$520=$51.43
但是,如果我们的解读是错误的,在我们下注时对手始终会弃牌,他的期望值就是$640。
(0.8)($800)=$640
当我们使用纳什均衡策略时,期望值就是$78.57。
$640-$571.43=$78.57
所以如果我们的解读是错误的,我们就会为自己的错误付出代价。
解读的价值
l 以情绪为导向的打法
l 对手特定的打法
l 数据/样本尺度的敏感性解读
比如,某人以9♣️8♦️在翻前进行全压,被跟注并不意味着他会一直用这手牌全压;很可能就是上头时的决定。尽管玩家在上头时可能有助于评估他的范围(可能比较宽泛),但玩家能够恢复冷静甚至可能利用自己形象的优势。
另外,玩家对手某人时的打法不一定会用来对抗你。他采取此类打法应该有他自己特定的解读,面对你时可能又有不同的解读,他的打法会随着玩家的不同而不同。
还有数据/样本尺度的敏感性解读。这类解读被赋予过多权重。你有多少次这样告诉自己,“那名玩家游戏了前面5手牌,他很松?”其实每一位玩家都有发挥得好的时候和发挥不好的时候。所以就算有人在一整个位置周期中加注每一手牌,说明他可能很松,也说明他就是恰好拿到了强劲的起手牌。幸运的是,使用概率理论,我们可以分析过这个并且找出对我们有用的马脚。
事实证明,一个相同的事件连续发生5次(在5个样本中)的概率可以通过简单地将各个事件的概率相乘来计算。所以我们计算出P(连续5次)=P(一次)5
这个公式是微不足道的,但它的影响却很大。绘制成图表如下:
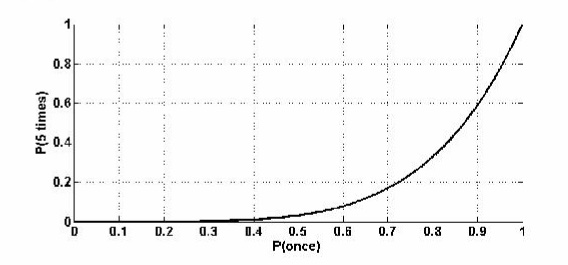
X轴上是一个事件发生一次的概率,Y轴上是同一事件连续发生5次的概率。我们看到,相对不可能发生一次的事件,极不可能连续发生5次,这可以应用于翻牌前的解读:
想象一下,某人的弃牌率为80%,那么他游戏手牌的概率就是20%。现在我们观察5手牌,每一手他都弃牌,发生这种情况的概率为33%。
0.33=(0.8)5
观察到他连续5次入局的概率要低得多,为3%。
0.032=(0.2)5
这是几个数量级的差异,尽管原来的概率处于同一个数量级。我们发现,如果我们遇到一名随机的、未知的对手,我们看到他连续5次弃牌,这可能并不意味着什么。但是,如果他连续玩了五手牌,我们就可以很肯定他的入池率高于20%!
因此,综上所述,对于对手的默认打法来说,一个事件发生的可能性越小,当该事件连续发生几次时,你得到的信息就越多。但如果该事件相当有可能会发生,比如放弃大多数起手牌,而且连续多次发生,你仍不会获得太多关于对手到底会如何游戏的信息。






评论 ( 0 )