第二节:石头剪刀布(RPS)
l 剪刀击败布
l 布击败石头
这真的就是一个A击败B,B击败C,C击败A的游戏。如果两人出一样的手势,那么此局就是平局。
RPS历史
RPS在历史上有一些有趣儿的运用。比如,2006年一名美国联邦法官要求对立双方通过RPS游戏来解决彼此争端。公开他自己的命令是为了羞辱那些以荒谬方式解决争议问题的律师事务所。
RPS甚至被大自然用来决定结果。常见的侧斑鬣蜥在其匹配策略上使用的就是RPS。雄性有三种不同的颜色。雌性根据橙色击败蓝色,蓝色击败黄色,黄色击败橙色的策略来选择配偶。目前尚不清楚平局是什么情况。
RPS博弈论
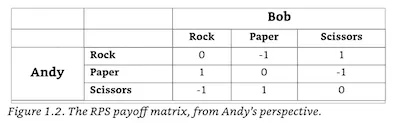
假设Andy在开始的时候一直都出石头(他是一名地质学家),Bob喜欢出布(他是一名伐木工人)。那么,在开始阶段,Andy一直都会输。这就是矩阵结果中的“-1”。
但Andy突然之间想通了,改出剪刀,此时他每次都会赢(+1)。最终Bob意识到他需要随机出3种手势中的一个,而自己赢的概率为1/3。
假设Andy的玩法是不均衡的,他选择石头的概率为35%,布的概率为33%,剪刀的概率为32%。Bob对于每一种手势的概率均为1/3。那么当Andy选择出石头时,Bob基本上都是输的。根据同样的算法,Andy选择出布或剪刀时,Bob能够实现收支平衡。
Bob的策略就是最佳博弈论。不论Andy采用什么策略,Bob从长远来看都能收支平衡,同时Andy也是。
当Bob使用他的GTO策略时,不管Andy采用什么策略都无法降低Bob的赢率。所以Bob对Andy的打法是无动于衷的。但是,如果Bob意识到Andy喜欢出石头,那么Bob就会偏离自己的GTO策略并选择频繁地出布。这就是一种剥削策略。
所以Bob有两种策略可供选择:
l 如果Andy实施GTO策略,那么Bob的策略就无关紧要了。从长远来看,没人会赢。
l 如果Andy偏离GTO策略,Bob就可以试图利用Andy的非GTO频率来实施剥削策略。
最佳策略
最佳博弈论并非是我们的最佳策略,它只是无法被剥削。
纯粹策略和混合策略
纳什均衡存在于当两名玩家都采用混合策略时,没有任何一方有利益动机去修改自己的策略。当纳什均衡存在时,每位玩家对于另一位玩家的具体行动都是无动于衷的。
对于RPS而言纳什均衡明显就是每位玩家随机选择出石头、布和剪刀,概率各1/3。于每位玩家来说这也是一种GTO策略。
有意思的地方在于你可以确切的告诉对手你的GTO策略是什么,从长远来看对手采取其他一些策略都是无法击败你的。你的GTO策略是无法被剥削的。
RPS中的剥削玩法
假设我们拥有很多RPS玩家的“对局历史”并可以分析每一位玩家的偏爱玩法。A玩家准备在下一局比赛中对阵KidRock选手,所以他查看了这位玩家的数据。A玩家发现KidRock实际上出石头的概率是35%,布的概率是33%,剪刀的概率是32%;他的玩法并不是那么的随机。A玩家仍然可以采取自己的GTO策略并在与KidRock对抗的过程中保持收支平衡。但如果A玩家通过出布的概率高于1/3从而偏离GTO打法,那么他会更有利可图。
如果比赛以单局定胜负,那么A玩家就应该选择出布来对抗KidRock。A玩家获胜的概率为35%,平局的概率为33%,败局的概率为32%。A玩家的期望值用公式表示就是(35-32)/(35+32) = +4.48%。
什么是平局?假设A玩家知道在平局后KidRock有80%的概率改变自己的选择,在布平局后KidRock出石头的概率远高于剪刀。所以A玩家会在平局后再次选择出布,在这个过程中获得额外的EV。A玩家利用KidRock的非GTO频率实施了一种剥削策略。
假设A玩家对抗的是一名新手,没有任何数据可参考。同样的,A玩家可以使用GTO策略并把控机会。但若假设他有10,000名玩家的RPS数据并知道玩家的平均数据是:石头的概率是35%,布的概率是33%,剪刀的概率是32%。那么A玩家就会知道一般玩家在平局过后改变自己选择的概率为80%,他们的新选择似乎都会基于上一局的选择而定。如果新手玩家碰巧使用了GTO策略,那么A玩家的策略就无关紧要了。但如果A玩家认为新手玩家的RPS心理是典型的,那么A玩家就可以利用剥削策略给自己提供优势。
与线上扑克对比应该是非常明显的。在很多网站,我们可以使用Heads-up Display (HUD),它能够提供特定对手的有用数据。对于那些我们一无所知的玩家,它能够为我们提供平局数据。(详见附页扑克数据ll)
在真正的牌局中,很少有玩家会使用GTO策略。所以,我们绝大多数有利可图的调整都是通过剥削对手的偏爱打法或至少普通对手来偏离GTO获得的。
RPS中最大限度的剥削打法
但如果KidRock出石头的概率是40%并且出剪刀的概率是60%呢?那么我们绝对输的概率就是20%。除非我们知道对手的全部策略而非仅仅一个单一的漏洞,那么我们就无法构建一个最大化的剥削策略。
让我们假设KidRock只有一些小小的漏洞,出石头//布/剪刀的概率分别是34%/33%/33%。我们知道他的全部策略,基于我们的对局历史。如果我们每次出布能赢$1,那么在100次对决后我们能收获$1。
但如果KidRock发现了这点不好的事情就会发生。如果KidRock在后面6次对决中都出剪刀,那么他就会成为绝对赢家。或者,如果他注意到自己的统计数据,他可能就会把自己的的概率变成30/37/33,这种变化太微妙以至于我们无法注意到,他会成为最后的赢家。
最大限度的剥削打法是一种脆弱的策略,如果对手捕获到了这个,那么就会很轻易被击破。
RPS中最低限度的剥削打法
让我们要求KidRock投掷一枚硬币,只要正面朝上他就必须出石头。但如果是反面,他可以出任何手势。同时也让我们假设他非常聪明,会以有利可图的方式随意抉择。
起初,我们也许会使用三种纯粹策略中的一种,每次都采取同样的抉择。如果我们100%出布,那么当KidRock出石头的时候,我们的赢率就是50%。但KidRock也非常聪明,能够通过可投掷的选项来反击我们,那么我们接下来的局面就是不输不赢。考虑到KidRock被迫出石头的限制,我们应该有更好的对策。
另外,我们可以100%的出石头。但KidRock能够通过硬币方面的选择来对我们进行反击,在这种情况下,我们平局的概率是50%,输的概率也是50%。于我们而言,这是一种输的策略。
最后,我们可以100%的出剪刀。KidRock可以通过硬币反面选择性地出石头回应我们,那么我们输的概率就是100%。
最好的打法就是混合策略,当然也包括混合一些纯粹策略。不管KidRock的应对策略是什么,我们的目标始终都该是+EV。
假设我们的混合策略中包括有一部分时间出剪刀。那么当KidRock出石头的时候,我们一定是输的,这个概率至少在50%;我们无法保持在不输不赢的状态,所以在我们的混合策略中绝不能出现剪刀。剪刀应该从我们的策略中剔除。
既然我们绝不会出剪刀,那么在非强制要求下他就绝不会出石头。于他而言,非强制环节该出什么也是一个受控策略。
所以我们对抗KidRock的混合策略只包括石头和布。但我们不能采用平局或让我们不输不赢的策略。因此,50/50石头/布的策略是不会有+EV,因为KidRock能够通过非强制性环节出剪刀来掰平局势。其实,我们采取的任何策略中出石头至少有50%的概率是能够被KidRock追成平局的。所以我们的策略中出石头的概率应该低于一半。
所以让我们计算一下最佳石头和布的策略。我出石头的时候EV用EV(R1)表示,也是KidRock出剪刀的频次(S2) 减去他出布的频次(P2),因为石头对石头是平局。当我们出布时的EV用EV(P1),KidRock出石头的频次减去他出剪刀的频次。公式如下:
EV(R1) = S2 – P2
EV(P1) = R2 – S2
博弈论中有一个原则叫作冷漠准则,也就是说这些EVs应该等于纳什均衡的结果。我们知道KidRock只有在被迫出石头时才会只出石头,R2 = 0.5,所以我们也应该知道P2 + S2 = 0.5。
通过解这个方程,我们可以得到:
R2=3/6
P2= 1/6
S2=2/6
我们可以运用同样的推理来找到自己的策略:
R1=2/6
P1=4/6
S1=0/6
所以,当KidRock在非强制性要求下以2/1比率出剪刀/布的时候,我们就以同样的比率出布/石头,此时纳什均衡就存在了。
我们这个游戏的EV是多少?当我们出石头时,我们的单位赢率是0-1/6+2/6 = 1/6。当我们出布时的赢率也是一样的。因此,我们的EV是2/6×1/6+4/6×1/6 = 1/6;KidRock的缺陷之处是有利于我们的。
所以对抗KidRock的最大限度剥削策略是难以知晓的,除非我们知道他的全盘RPS玩法。如果我们总是出布,KidRock能够有效地对抗我们的策略。这是一个脆弱的策略。
在Sutherland的RPS游戏中,规则要求KidRock出石头的概率为50%。所以针对该游戏的GTO解决方案是一种真正的纳什均衡。但如果我们根据标准的RPS游戏规则来,KidRock还是需要50%的时候必须出石头,那么上面的解决方案就不是一种真正的GTO解决方案。(这部分内容可能有语意上的歧义,因为我们仍需要使用博弈论来构建解决方案。)
相反,这种解决方案被视为最底限度剥削策略更为恰当,一种剥削KidRock不足之处的策略,但也不是一种轻易剥削策略。如果KidRock发现了我们的玩法,那么他就可以调整自己的策略来实现+EV对抗我们。
扑克的类比应该是很明显的。人工智能电脑程序能够计算出一对一德州扑克的GTO解决方案。它也可以跟踪人类对手的实际行动和构建最低剥削策略来提升自身的EV。修正后的策略不再是一个真正的GTO解决方案,但确是一个基于博弈论的策略。这就是一些GTO电脑可以完成的事。
我将指出一个RPS并未转换成扑克的属性。当我们在RPS中采用一个GTO策略时,不管对手的策略多么差劲,我们都会有个不输不赢的局面。坏人没有真正的机会去犯错或犯一个愚蠢的错误。
但在扑克中,当一个人偏离他自己的GTO选择时,他会输很多钱给一名GTO玩家。这主要取决于他实际犯的是哪类错误。如果对手犯的是愚蠢的错误,他在对抗一个GTO策略时会有一个负的EV。(一个愚蠢的错误包括在还没有接近钱圈泡沫时在翻前就弃掉A。但它也可能包括不太明显的错误。)






评论 ( 0 )